Um cubo isolante de aresta encontra-se uniformemente carregado em todo o seu volume e possui uma carga total . Desenha-se, então, uma superfície fechada , também cúbica e de aresta , concêntrica ao cubo original e com faces paralelas ao mesmo, como mostra a figura abaixo.
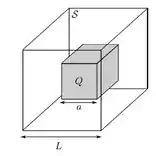
Sobre esse sistema, considere as afirmativas abaixo:
- O fluxo do campo elétrico produzido pelo cubo através de tem módulo igual a .
- O campo elétrico produzido pelo cubo tem a mesma direção em todos os pontos de uma das faces de .
- O campo elétrico produzido pelo cubo tem o mesmo módulo em todos os pontos de .
São corretas as afirmativas:
- Somente e
- Somente
- Somente
- Somente e
- Somente e
- Somente
- , e
- Nenhuma delas.
Passo 1
Aqui, a nossa superfície gaussiana (superfície fechada!) é um cubo e dentro desse cubo, temos uma carga total positiva igual a . Por isso, quando aplicamos a lei de Gauss, temos que o fluxo do campo elétrico é dado por:
Portanto, o item está CORRETO.
Passo 2
Para matarmos os próximos itens, vamos olhar para a figura abaixo. Vemos que existem pontos da superfície fechada que estão a distâncias diferentes da carga . Por exemplo, olhando para a figura, as retas em azul, que representam os vetores campos elétricos, são perpendiculares às arestas do cubo de carga e os pontos em que eles tocam a superfície estão à mesma distância de .
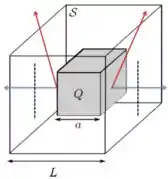
Por outro lado, os vetores em vermelho, que estão no mesmo plano das azuis, mas inclinadas em relação a estas, atravessam os pontos das “quinas” do cubo que estão a uma distância maior do cubo . Disso, concluímos que o módulo campo elétrico nesses pontos é menor do que aquele que a carga produz nas posições onde as retas azuis tocam as faces de .
Por isso, o item está INCORRETO.
Dessa mesma figura e com os mesmos vetores desenhados, a gente também conclui que as direções desses vetores mudam no diferentes pontos da superfície gaussiana .
Por essa razão, o item também está incorreto.
Resposta
Letra f).