Um fio infinito, isolante, com densidade linear de carga uniforme , é colocado sobre uma placa infinita, isolante, com densidade superficial de carga uniforme .
Utiliza-se um sistema de coordenadas cartesianas tal que o fio está ao longo do eixo e a
placa se extende no plano , conforme a figura.
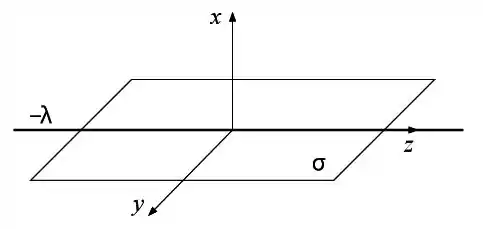
Calcule o vetor campo elétrico produzido pela placa em todo o espaço.
Calcule o vetor campo elétrico produzido pelo fio em todo o espaço.
Determine os pontos do espaço onde a força que atua sobre uma partícula de carga Q é nula.
Passo 1
Para calcular o vetor campo elétrico produzido pela placa vamos utilizar a lei de Gauss e para isso vamos escolher um cilindro como superfície fechada (superfície gaussiana) para aplicarmos a lei de Gauss.
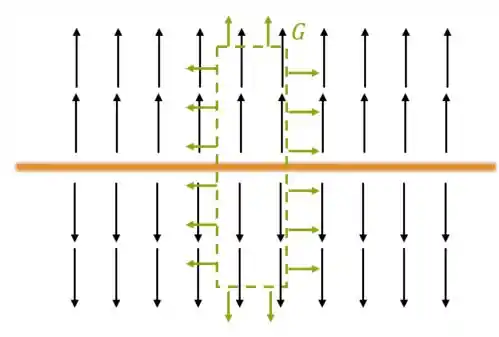
Porque com essa superfície vamos simplificar os cálculos.
Pois o fluxo de campo elétrico pela lateral é zero. Assim, temos fluxo apenas nas tampas.
Como o campo é constante e temos duas tampas,
Como a integral é
Temos,
Isolando o campo elétrico,
Temos que a carga da placa é dada por
Então,
Passo 2
Faremos o mesmo para o calculo do campo elétrico gerado por um fio, porém nesse caso o fluxo de campo elétrico será zero nas tampas da superfície cilíndrica.
Como
Assim, temos
Sendo que
Logo
Passo 3
A força só será nula quando o campo elétrico for nula nela. Assim, iremos procurar os pontos onde o campo elétrico do fio anula os da placa, para isso naquele ponto eles devem ser iguais.
Para que os campos se anulem, eles devem estar na mesma direção, e isso acontecerá apenas no plano , logo . E como nenhum dos campos dependem da coordenada , então o valor de pode ser qualquer um.
Então vamos analisar para e para , pois o campo elétrico da placa depende do sinal de . Começando para :
Agora, faremos o mesmo para :
Então os pontos são