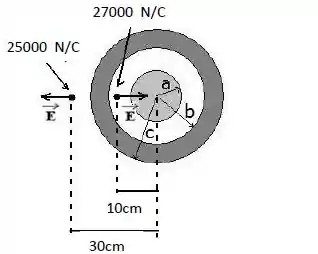
A figura mostra uma esfera metálica e maciça posicionada no centro de uma outra esfera metálica oca. (Na figura, , e )
.
Qual é a carga total distribuída na superfície externa da esfera oca?
;
;
;
;
;
Passo 1
Esse problema aqui é meio o inverso. Geralmente a gente calcula o campo elétrico a partir das cargas. Agora temos o campo elétrico e tempos que calcular as cargas a partir dele
Pela lei de Gauss e como o sistema tem simetria esférica temos que:
Pela simetria esférica, e escolhendo como gaussiana uma esfera de raio , essa integral fica
Como
Agora temos que analisar cada uma das regiões
Passo 2
Se pegarmos uma esfera de raio , onde , a carga total dentro dessa esfera será a carga da esfera metálica maciça. Pela figura da questão o campo elétrico pra essa distância é , assim
Passo 3
Agora vamos pegar uma esfera de raio , onde . A carga total dentro dessa esfera será a carga da esfera maciça somada com a carga da esfera oca. Assim
Substituindo os valores, teremos:
Passo 4
Já temos as cargas das duas esferas, mas precisamos da carga na superfície externa da esfera oca. Como a esfera oca é metálica somente teremos carga nas superfícies interna e externa da esfera, ou seja
Onde é a carga na superfície interna (de raio ) e é a carga na superfície externa (de raio ).
Como já temos , precisamos de .
Pra isso vamos desenhar agora uma gaussiana de raio , onde , ou seja, uma gaussiana que está dentro da esfera oca. A carga total dentro dessa gaussiana é
E o campo elétrico dentro da esfera oca é nulo, já que a esfera é metálica.
Assim, pela lei de Gauss
Passo 5
Como
Finalmente podemos calcular a carga na superfície externa da esfera oca
Resposta
(E)