. Um cabo coaxial simples consiste de um cilindro condutor maciço, infinito, de seção transversal circular de raio e uma casca condutora cilíndrica, infinita e coaxial ao cilindro, de raio interno e raio externo . O cilindro possui uma quantidade de carga por unidade de comprimento ao longo do eixo igual a e a casca possui uma quantidade de carga por unidade de comprimento igual a , onde é uma constante positiva. Nessa situação, podemos afirmar que a densidade superficial de carga na superfície interna da casca e o módulo do campo elétrico a uma distância do eixo comum, tal que , valem, respectivamente:
Escolha uma opção:
e
e
e
e
e
e
e
e
Passo 1
Vem comigo que a gente resolve essa juntos!
Primeiro vamos visualizar o que temos em mãos, o cenário que o enunciado descreveu é o seguinte:
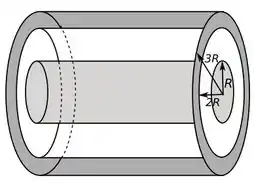
Temos que encontrar a densidade de carga superficial da superfície interna da casca de raio que o enunciado pede.
Densidade de carga superficial é dada por carga por área, então teríamos que:
Mas como vamos mexer com a área de uma coisa que infinita? Vamos contornar isso usando o fato de que a carga é distribuída igualmente por essa superfície.
Então podemos considerar um trecho de comprimento da superfície interna e fazer essa análise para ela e isso vai ser o mesmo para qualquer parte da superfície.
Para encontrar o campo elétrico na região , que é a região entre o cilindro e a casca, vamos usar a lei de Gauss, dada por:
Para aplicar essa lei, vamos usar uma superfície cilíndrica de comprimento e raio fechada que engloba o cilindro, o elemento de área vai ser perpendicular a superfície lateral desse cilindro que imaginamos, logo ela vai ser paralela a , assim:
A carga interna vai ser a carga dentro do nosso cilindro de comprimento .
Agora que temos tudo o que precisamos, vamos as contas!
Passo 2
Vamos começar com a densidade superficial de carga.
Temos que:
Como já falamos no passo , vamos considerar um pedaço da superfície de comprimento , como temos a densidade linear de cargas dessa casca, a carga nesse pedaço é dada por:
A área desse pedaço de superfície vai ser o mesmo que a área da superfície de um cilindro de raio , assim:
Então temos que:
Ponto, temos a densidade que queríamos.
Passo 3
Agora vamos calcular o campo na região que queremos. Temos o seguinte da lei de Gauss.
Como o campo de um cilindro é homogêneo, temos:
Essa integral em é igual a área do cilindro de comprimento e raio que estamos considerando, assim:
A carga interna já que temos a densidade linear de carga, vai ser dada por , assim:
Prontinho, temos o campo que queríamos, assim a nossa alternativa vai ser a letra .
Resposta
e