Duas cascas esféricas finas e condutoras concêntricas de raios e possuem cargas e , como indicado abaixo.
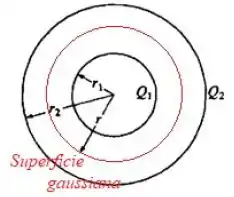
Considere a região onde é à distância até o centro das esferas. Nessa região, o campo elétrico resultante é:
Passo 1
Beleza, esse é um problema clássico de Lei de Gauss, que é dada por:
A ideia aqui é a seguinte, vamos aproveitar a simetria esférica do problema e escolher uma gaussiana também esférica.
Fazendo isso, garantimos, em todos os pontos da gaussiana, que o módulo do campo elétrico é constante, e que os vetores e são paralelos. Como resultado, podemos escrever a Lei de Gauss da seguinte forma:
Onde corresponde à área da superfície gaussiana.
Passo 2
A nossa gaussiana com raio está englobando somente a casca esférica de carga , dessa forma:
Substituindo na expressão do campo elétrico:
Resposta