Determine o campo elétrico produzido por um plano infinito com uma distribuição de carga uniforme positiva por unidade de área igual à .
Passo 1
Primeiramente um desenho para ilustrar o aspecto do campo de um plano infinito carregado. Sabemos, pois decoramos, que ele é uniforme e estacionário (na primeira prova tudo é estacionário):
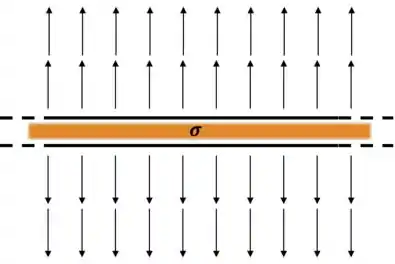
Passo 2
Agora enunciamos a lei de Gauss para tentar calcular o campo elétrico:
Escolhendo uma Gaussiana cilíndrica (prisma), podemos simplificar o cálculo do fluxo:
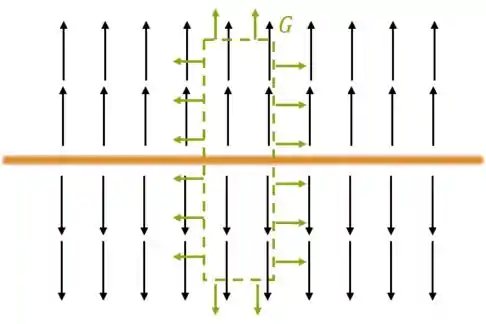
Como os vetores normais são perpendiculares ao campo na lateral, temos somente o fluxo correspondente às tampas. Tenham elas área igual à :
Passo 3
Pela configuração do campo, ele tem módulo constante em toda , portanto:
Substituindo:
A integral de nas tampas é igual à área delas :
Portanto o campo é:
Passo 4
Agora precisamos nos livrar dessa carga interna à Gaussiana, que é uma quantidade desconhecida. Como a densidade é constante, temos:
Logo:
Podemos então substituir:
Que resulta em:
E o módulo do campo é este. Se fosse pedido o vetor campo, precisaríamos de alguma espécie de sistema de coordenadas para poder especificar a direção deste, pois acima do plano carregado o vetor aponta para cima e abaixo do plano o vetor aponta para baixo. Se fosse o caso de termos um eixo alinhado ao campo, teríamos:
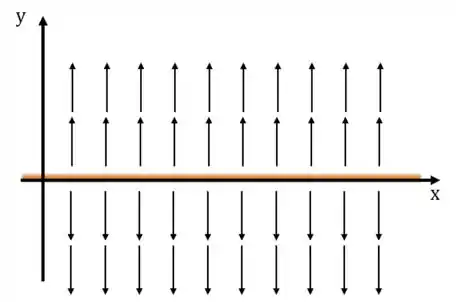
De onde segue: