Um cilindro circular, muito longo, possui uma densidade volumar de carga elétrica estacionária, mas não uniforme , onde e é a usual coordenada radial, medida a partir do eixo de simetria do cilindro.
Envolvendo tal cilindro, temos uma casca cilíndrica circular espessa, coaxial, também muito longa, de raios interno e externo , condutora e neutra.
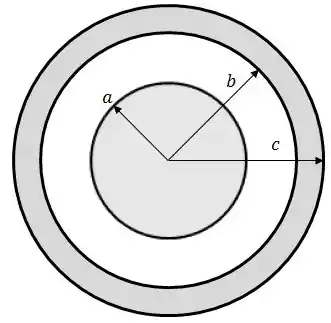
Determine a carga por unidade de comprimento axial, no cilindro interno.
Determine o campo elétrico em um ponto genérico dentro do cilindro interno, com coordenada radial .
Determine o campo elétrico em um ponto genérico na região entre os dois cilindros, com coordenada radial .
Determine o campo elétrico em um ponto genérico dentro da casca condutora, com coordenada radial .
Determine o campo elétrico em um ponto genérico na região exterior aos dois cilindros, com coordenada radial .
Passo 1
Determine a carga por unidade de comprimento axial, no cilindro interno.
A carga está associada com a densidade volumétrica de carga por:
Como a densidade volumétrica de carga varia com o raio, o elemento será dado por:
Substituindo e na expressão de , teremos:
Assim, a carga por unidade de comprimento axial será:
Passo 2
Determine o campo elétrico em um ponto genérico dentro do cilindro interno, com coordenada radial .
O campo elétrico é determinado através da lei de Gauss, dada por:
Nesse caso, a nossa gaussiana será um cilindro com o mesmo comprimento do cilindro da questão. Logo:
Por conta da simetria do problema, o campo elétrico tem direção radial, logo:
Agora precisamos calcular a carga interna aqui
Passo 3
Vamos fazer aqui, basicamente, a mesma coisa que fizemos no item , a diferença agora é que vamos integrar de a , logo:
Substituindo esse cara na expressão do campo elétrico, teremos:
Passo 4
Determine o campo elétrico em um ponto genérico na região entre os dois cilindros, com coordenada radial .
Novamente, o campo elétrico vai ter essa cara:
A diferença aqui é que agora a carga englobada pela gaussiana é toda a carga da cilindro interno, logo:
Logo:
Passo 5
Determine o campo elétrico em um ponto genérico dentro da casca condutora, com coordenada radial .
Aqui vai uma coisa que você tem que me prometer que vai guardar contigo: no equilíbrio eletrostático, o campo elétrico no interior de um material condutor é sempre nulo.
Sendo assim, como a região está no interior da casca condutora:
Passo 6
Determine o campo elétrico em um ponto genérico na região exterior aos dois cilindros, com coordenada radial .
Já sabemos que o campo elétrico tem essa cara:
Agora, a carga envolvida pela gaussiana é a carga do cilindro interno e da casca cilíndrica, logo:
Logo:
Resposta