O campo elétrico representado na figura está dirigido ao longo do eixo . Ele é uniforme nas direções e , mas sua intensidade varia em função de (em outras palavras ).
Considere uma superfície fechada cilíndrica de raio e comprimento como ilustrado na figura.
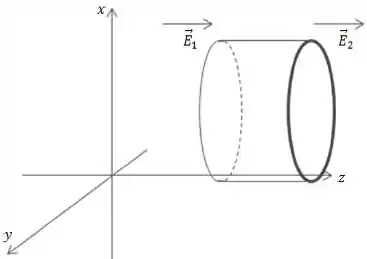
As intensidades do campo elétrico nos lados esquerdo e direito do cilindro são, respectivamente, e . A carga elétrica envolvida pelo cilindro é dada por:
;
;
;
;
;
Passo 1
Através da Lei de Gauss, temos que:
Considerando o nosso cilindro como gaussiana, podemos ver na figura que as que o campo elétrico atravessa o cilindro apenas nas bases circulares.
Como a área é constante, a Lei de Gauss será dada por:
Reorganizando, vemos que a carga será dada por:
A resposta certa é a letra .
Resposta
;
Exercícios de Livros Relacionados
A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui