Um fio finito muito longo de comprimento e carregado com uma carga está no eixo de um cano cilíndrico condutor descarregado de raio interno , raio externo e mesmo comprimento .
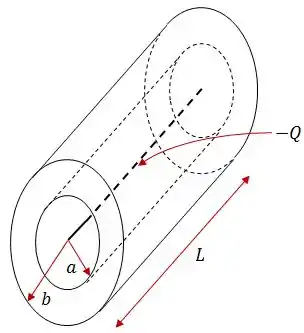
Que cargas aparecem nas superfícies interna e externa do cano?
Utilize a Lei de Gauss para calcular o vetor campo elétrico para , e ;
Passo 1
a) Que cargas aparecem nas superfícies interna e externa do cano?
O que acontece aqui é que, quando colocamos o fio com carga no interior do cano cilíndrico, o fio atrai as cargas positivas do cano para a superfície interna e repele as cargas negativas do cano para a superfície externa.
No equilíbrio eletrostático, a carga da superfície interna deve ser, necessariamente:
Entretanto, o cano deve manter a sua carga inicial, que nesse caso é zero (já que está descarregado).
Assim, a soma das cargas da superfície interna e da superfície externa deve ser igual a zero. Logo:
Passo 2
b) Utilize a Lei de Gauss para calcular o vetor campo elétrico para , e ;
A Lei de Gauss é dada por:
Simplificando a Lei de Gauss, teremos:
Onde é a área da nossa gaussiana, por onde passará o campo elétrico. Como se trata de uma geometria cilíndrica, a gaussiana será um cilindro de raio e comprimento , cuja área será dada por .
Logo:
Pra finalizar, como estamos trabalhando com geometria cilíndrica, o campo elétrico terá sempre direção radial. Assim:
Agora, o nosso trabalho é determinar a carga interna à gaussiana para cada situação.
Passo 3
-
Essa região engloba somente o fio carregado, logo:
Assim, o campo elétrico será dado por:
Passo 4
-
Essa região engloba o fio carregado e a superfície interna do cano cilíndrico, logo:
Logo:
Passo 5
-
Essa região engloba o fio carregado e o cano cilíndrico descarregado, logo:
Assim:
Resposta
a)
b)
-
-
-