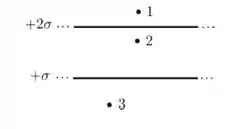
Dois planos infinitos e paralelos encontram-se uniformemente carregados com densidades superficiais de carga e , como mostrado na figura abaixo. Sejam , e os módulos do campo elétrico resultante produzido pelos dois planos nos pontos 1, 2 e 3 indicados na figura, respectivamente. Nessa situação, podemos afirmar que:
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
Passo 1
Vamos calcular o campo de cada plano separado e depois juntamos eles, ok?
Primeiro, o plano de cima.
Usando lei de gauss com simetria planar, temos que, o campo vale , saindo da placa.
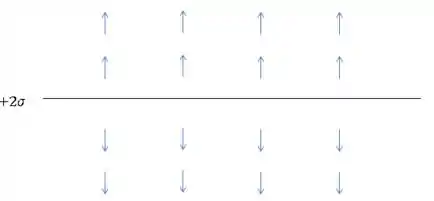
OBS.1) Uma coisa importante é notar que abaixo do plano, o campo vai apontar para “baixo” em todo o espaço. E acima do plano ele vai apontar para cima, em todo o espaço.
Agora, para o plano de baixo. Pela lei de gauss, com simetria planar, encontramos que o campo é saindo da placa. Ou seja:
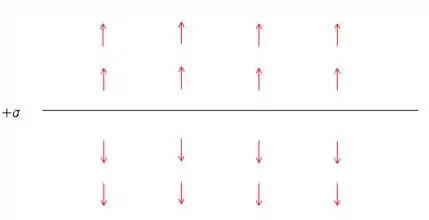
OBS.2) Uma coisa importante é notar que abaixo do plano, o campo vai apontar para “baixo” em todo o espaço. E acima do plano ele vai apontar para cima, em todo o espaço.
Notem que o módulo do campo em vermelho é menor do que o módulo do campo azul, pois as densidades superficiais são diferentes.
Agora, vamos juntar eles. Pelo principio da sobreposição podemos somar, vetorialmente, os campos. Então:

Notem, que ao sobrepor as imagens aquelas observações que eu escrevi tem que ser satisfeitas.
Agora, podemos ver que, no ponto 1, temos os campos vermelho e azul apontando pra cima (vamos considerar esse sentido como positivo, ok?). dessa forma:
Na região 2, temos os campos em direções opostas, então
Ah, ele fala que e são os módulos dos campos naqueles pontos, então.
E agora, na região 3, temos os dois campos apontando pra baixo.
Então
Como estamos falando de módulo, temos:
Comparando os três, temos:
Resposta
Letra A).