Seja um fio isolante fino (que pode ser considerado reto e infinito) carregado com uma densidade linear de carga uniforme . Este fio está colocado paralelamente e concentricamente com um cilindro condutor (também infinito), de raio interno e raio externo , como mostra a figura 1 abaixo. O cilindro condutor possui, inicialmente, uma densidade linear de carga uniforme .

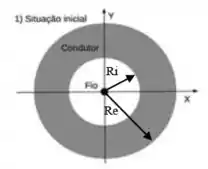
1. Calcule as densidades superficiais de carga e , respectivamente, nas superfícies interna e externa do cilindro, considerando que o equilíbrio eletrostático foi atingido.
2. Calcule o campo elétrico nas regiões , e .

Agora suponha o cilindro anterior seja substituído por um cilindro isolante, com dimensões idênticas e com exatamente a mesma distribuição de cargas que nos itens a) e b). O mesmo fio usado anteriormente é, então, deslocado ao longo do eixo , de modo que seu centro se encontra agora em , como mostrado na figura 2 abaixo.

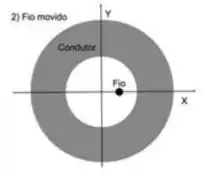
c) Calcule o campo elétrico no ponto .

b) Para calcular o campo elétrico, podemos usar superfícies gaussianas cilíndricas, dado que a simetria do campo é cilíndrica, pois o campo aponta do eixo central para fora, radialmente. Assim, temos que, para um raio , o fluxo total é

Portanto,

- Na região , , então

- Na região , , pois está dentro do condutor ;

- Na região , , então

c) O campo no ponto , equivale a subtrair o campo do fio localizado em por um campo do mesmo fio localizado em : se notar que é só subtrair o antigo e adicionar o novo:

Portanto,