Um bastão cilíndrico isolante, de comprimento e raio (com ), foi carregado uniformemente em sua superfície com carga negativa desconhecida (Figura 1). Mediu-se o campo elétrico gerado a uma distância do eixo de simetria e encontrou-se o valor (em módulo).
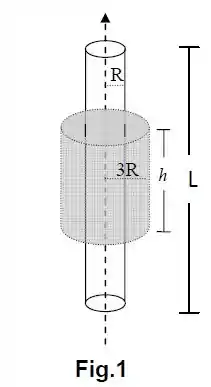
Calcule o fluxo do campo elétrico através da superfície indicada (sombreada) na Figura 1 (altura e raio ).
Obtenha o vetor campo elétrico em função da distância ao eixo do bastão, para .
Suponha agora que uma casca cilíndrica condutora descarregada (neutra) de comprimento e raios interno e externo é colocada em volta do bastão carregado utilizando-se luva de borracha. Posiciona-se a casca com o eixo de simetria coincidindo com o eixo do bastão (concêntrico), conforme a Figura 2.
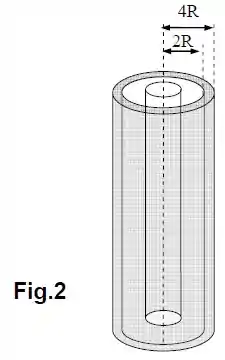
Responda, justificando:
Obtenha o valor (módulo) do campo elétrico à distância do eixo.
Quanto vale a carga na superfície interna e na superfície externa da casca cilíndrica?
Agora suponha que a casca cilíndrica condutora seja aterrada. Responda, justificando:
Quanto vale a carga na superfície interna e na superfície externa da casca cilíndrica?
Calcule o fluxo elétrico que atravessa uma superfície cilíndrica concêntrica ao sistema e de raio .
Passo 1
Calcule o fluxo do campo elétrico através da superfície indicada (sombreada) na Figura 1 (altura e raio ).
Por definição, o fluxo elétrico é dado por:
Dada a geometria do problema, o campo elétrico estará na direção radial, sendo perpendicular à superfície cilíndrica e paralelo ao vetor .
O enunciado já nos disse que o módulo do campo nessa superfície é e como a barra está carregada negativamente, o campo elétrico tem sentido de fora para dentro na direção radial. Isso significa que o fluxo elétrico é negativo.
Assim, podemos simplificar a expressão do fluxo elétrico para:
Onde a área lateral do cilindro é dada por .
Passo 2
Obtenha o vetor campo elétrico em função da distância ao eixo do bastão, para .
Essa é uma questão clássica de Lei de Gauss, dada por:
Dada a simetria cilíndrica do problema, podemos simplificar a Lei de Gauss para:
Onde a área é a área lateral do cilindro, dada por:
Portanto:
A dúvida agora é a seguinte: “Como vamos descobrir quem é ?!”.
Passo 3
A malandragem aqui é saber que a Lei de Gauss calcula o fluxo elétrico através de uma superfície fechada. Basicamente o que fizemos na , ou seja:
Opa! O fluxo elétrico nós já sabemos, certo?
Onde, agora, ao invés de , usaremos , que corresponde à altura da barra:
Agora ficou tranquilo! Só temos que substituir essa expressão de na expressão do campo elétrico que já tínhamos encontrado no passo anterior.
Simplificando esse cara:
Passo 4
Obtenha o valor (módulo) do campo elétrico à distância do eixo.
Beleza! Agora estamos olhando para a Figura 2.
A uma distância do eixo, a região encontra-se no interior do condutor. Opa! Aqui vai uma para que você tem que guardar contigo sempre: no interior de um condutor, o campo é sempre nulo!
Logo:
Passo 5
Quanto vale a carga na superfície interna e na superfície externa da casca cilíndrica?
Como o condutor é neutro, quando colocarmos o bastão carregado negativamente no interior da casca cilíndrica, as cargas positivas do condutor serão atraídas e vai se acumular na superfície interna do condutor.
Da mesma forma, as cargas negativas do condutor serão repelidas e se acumularão na superfície externa.
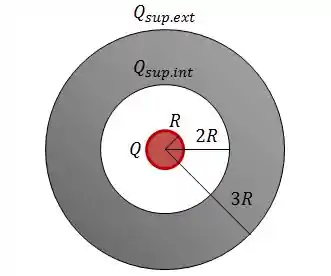
No equilíbrio eletrostático, os módulos das cargas devem ser iguais, mas seus sinais devem ser opostos, conforme discutimos ali em cima:
Onde a carga do bastão nós já calculamos na letra .
Como o condutor é neutro:
Passo 6
Quanto vale a carga na superfície interna e na superfície externa da casca cilíndrica?
Se o condutor for aterrado, apenas a carga de sua superfície externa é modificada e cai necessariamente a zero.
Portanto:
Isso significa que, agora, o condutor passará a ficar carregado positivamente.
Passo 7
Calcule o fluxo elétrico que atravessa uma superfície cilíndrica concêntrica ao sistema e de raio .
Opa! Já vimos que podemos associar o fluxo elétrico com a Lei de Gauss:
Logo:
Quando , a região em que queremos calcular o campo elétrico engloba tanto o bastão quanto a casca cilíndrica. Sendo assim:
Portanto:
Resposta