Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Lei de Gauss – Simetrias

Ver Teoria
Exercício 481234567891011121314151617181920212223242526272829303132333435363738394041424344454647495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Considere uma casca esférica isolante de raio interno a e raio externo b , conforme a figura. Na região a < r < b , a casca esférica tem uma densidade volumétrica de carga ρ ( r ) = c r , onde c > 0 e r é a distância até o centro da casca esférica. Coloca-se no centro da casca esférica uma carga q

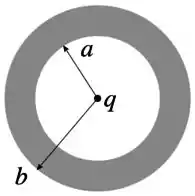
(a) Calcule o vetor campo elétrico na região a < r < b .

(b) Calcule o vetor campo elétrico fora da casca (região onde r > b ).

(c) Suponha agora que a casca esférica é condutora ao invés de isolante, com carga total Q . Mantendo a carga q no centro da casca, quais seriam os valores das cargas na superfície interna ( r = a ) e na superfície externa ( r = b )?

Passo 1

Temos que por simetria o campo elétrico vai estar na direção radial, ou seja, E → = E ( r → ) r ^ . Isso significa que o cálculo do fluxo do campo elétrico em uma superfície esférica fechada centrada em q é moleza de resolver

∮ E → . d A → = ∮ E r → . d A = E r → 4 π r 2

Passo 2

Sabemos pela lei de Gauss que a integral em uma superfície fechada é igual a toda carga dentro da superfície fechada dividido por ϵ 0 .

Dessa forma

∮ E → . d A → = q d e n t r o ϵ 0

Queremos saber o campo a uma distância a < r < b e para isso temos que saber o total de carga nessa região.

Para a carga total teremos duas contribuições:

- A carga pontual q no centro da esfera

- A carga contida na casca esférica

Assim a carga total será

q d e n t r o = q + ∫ ρ r d V

Essa última integral será (lembrando que d V = s e n θ r 2 d r d ϕ d θ

∫ ρ r d V = ∫ 0 π s e n θ d θ ∫ 0 2 π d ϕ ∫ a r c r ' r ' 2 d r '

∫ ρ r d V = 4 π c r ' 4 4 r ' = a r ' = r = π c r 4 - a 4

Assim q d e n t r o = q + π c r 4 - a 4

Passo 3

Agora podemos aplicar a lei de Gauss

∮ E → . d A → = q d e n t r o ϵ 0

E r 4 π r 2 = q + π c r 4 - a 4 ϵ 0

E → r = q + π c r 4 - a 4 4 π ϵ 0 r 2 r ^

Não se esqueça de no final indicar que o campo elétrico é um vetor e que ele está na direção radial!

Passo 4

Quando r > b a superfície gaussiana contém toda a carga da casca esférica e a carga pontual no seu centro. Dessa forma, o cálculo da carga total é igual ao que fizemos antes, só que agora integrando até b . Assim

q d e n t r o = q + π c b 4 - a 4

E da mesma forma o campo será dado por

∮ E → . d A → = q d e n t r o ϵ 0

E r 4 π r 2 = q + π c b 4 - a 4 ϵ 0

E → r = q + π c b 4 - a 4 4 π ϵ 0 r 2 r ^

Passo 5

Agora vamos supor que a casca esférica é condutora com carga total Q e que no seu centro oco ainda temos a carga q .

O que muda aqui? Dentro de um condutor o campo elétrico é nulo devido a um rearranjo de cargas e só poderá haver cargas nas superfícies interna ( r = a ) e externa ( r = b ) .

Como o campo elétrico dentro do condutor é nulo, se escolhermos uma superfície gaussiana que esteja totalmente dentro do condutor, teremos que o fluxo do campo elétrico nessa superfície será nulo. Pela lei de Gauss isso significa que a carga total dentro dessa superfície é nula, ou seja

∮ s u p e r f í c i e c o n d u t o r a   E → . d A → = ∮ s u p e r f í c i e c o n d u t o r a   0 . d A → =   q d e n t r o ϵ 0 → q d e n t r o = 0

Para capturar a superfície interna, vamos escolher uma superfície esférica de raio a < r < b . Sabemos que a carga total dentro dessa superfície é nula e que suas componentes são a carga q no centro da esfera e a carga q a na interface r = a . Assim

q + q a = 0 →   q a = - q

Por outro lado, sabemos que a carga total da casca esférica é Q . Como chamamos a carga na interface r = a de q a vamos chamar a carga na interface r = b de q b . Dessa forma

Q = q a + q b = - q + q b

q b = Q + q

Resposta

  1. E → r = q + π c r 4 - a 4 4 π ϵ 0 r 2 r ^
  2. E → r = q + π c b 4 - a 4 4 π ϵ 0 r 2 r ^
  3. Superfície interna ( r = a ) -> q a = - q

Superfície externa ( r = b ) -> q b = Q + q  

Exercícios de Livros Relacionados

A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui