Considere um disco circular isolante fino, de raio , carregado com uma carga total uniformemente distribuída sobre sua superfície. Desenha-se, então, uma superfície imaginária , fechada, na forma de um cilindro circular reto de raio , comprimento e eixo coincidente com o eixo do disco. Suas tampas são paralelas ao disco e equidistantes dele. Sobre essa situação, considere as afirmativas abaixo:
- O fluxo de campo elétrico produzido pelo disco através de é igual a .
- O campo elétrico produzido pelo disco tem a mesma intensidade em todos os pontos sobre a superfície lateral do cilindro.
- O campo elétrico produzido pelo disco tem a mesma intensidade em todos os pontos sobre as tampas do cilindro.
São VERDADEIRAS as afirmativas:
- e
- e
- e
- , e
- Nenhuma delas.
Passo 1
Nessa questão, galera, acho que vai ser bom fazermos uma breve revisão de como é o campo elétrico produzido pelo disco com carga uniformemente distribuída num ponto arbitrário, como aquele ilustrado na figura abaixo. Colocamos o eixo de simetria do disco coincidindo com o eixo e queremos saber como é o campo num ponto qualquer, que está a uma distância do centro do disco.
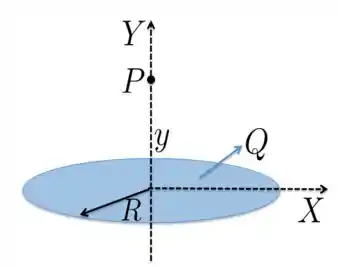
Agora, qual o valor do campo elétrico no ponto ? Bom, como o objetivo desta questão não é encontrarmos explicitamente este valor, vamos recorrer ao nosso material aqui do Responde Aí para pegarmos a expressão desse campo, que tem a seguinte “cara”
Conselho? Tenta revisar como que se encontra essa expressão, porque isso vai te ajudar em outras questões que envolvam integração. Aqui, como o objetivo é outro, vamos apenas analisar essa expressão para estudar os itens do problema.
Para esta questão, você precisa se lembrar apenas de algumas características desse campo. Não lembra de nenhuma delas? Vamos lá, te ajudamos...
Primeira coisa: esse cálculo foi feito para pontos que estão sobre o eixo de simetria do disco, correto? Sobre um ponto genérico desse eixo. Blz! Fica claro da equação acima que o campo elétrico depende de , ou seja, da distância entre o ponto arbitrário e o centro do disco.
Segunda coisa: o campo elétrico, neste eixo de simetria, tem componente apenas na direção , blz?
Até aqui, tá tudo OK?? Continuemos...
Passo 2
Agora, por que chamei sua atenção para o caso da figura acima? Segue este passo abaixo e verás... ;-) Você vai ver que Passo 1 é importante para a sequência...
Vamos “vestir o disco” com carga com uma superfície gaussiana cilíndrica, como mostra a próxima figura. Toda a carga está dentro do cilindro de altura .
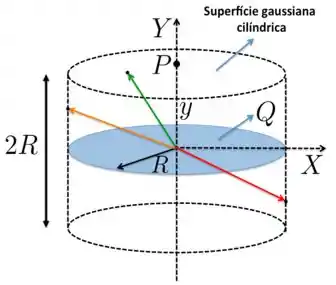
Agora, dá uma olhada nos vetores em verde, laranja e vermelho na figura. Como seriam os campos elétricos resultantes gerados por nessas posições? Você vê que fica mais difícil calcular esses campos explicitamente, mas podemos concluir algumas coisas gerais sobre eles.
Por exemplo, nessas posições, o campo elétrico também vai depender de e, além disso, pode ter componentes em também. Isto é, em pontos como esses sobre a tampa do cilindro (vetor em verde) e sobre as suas laterais (vetores em laranja e vermelho), o campo pode depender tanto de quanto de e, por isso, é diferente em cada um dos pontos sobre as superfícies laterais e sobre a tampa da superfície gaussiana!
Isso já te ajuda a julgar os itens e do problema, que estão INCORRETOS!!
Passo 3
Continuando...
Lembra que no comecinho do Passo 2 colocamos a seguinte frase: Toda a carga está dentro do cilindro de altura Pois é, agora a gente resolve o item com facilidade!! Por quê? Lei de Gauss, meus caros, lei de Gauss...
A lei de Gauss afirma que:
onde é o fluxo do campo elétrico através de uma superfície fechada e é a carga líquida no interior dessa superfície gaussiana. Então, no caso da figura acima, qual é a ? Resposta: ! Portanto, o fluxo elétrico é:
o que mostra que o item está correto!
Resposta
Portanto, apenas o item é verdadeiro. Por isso, a resposta é letra a) .