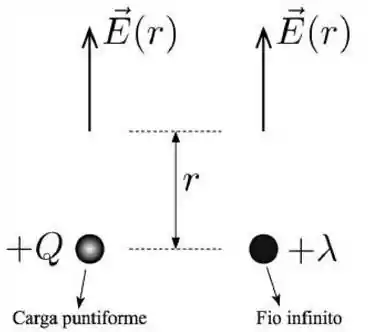
Uma carga puntiforme positiva e um fio infinito carregado positivamente com densidade de carga estão ilustrados na figura abaixo. A direção do fio é perpendicular à folha de papel. Considere os campos elétricos gerados pelos dois objetos em função da distância de cada um deles. Para qual distância os campos elétricos gerados são idênticos:
(a)
(b)
(c)
(d)
(e)
Passo 1
Primeiramente, vamos lembrar a definição a lei de Gauss na forma integral.
Esta lei diz que o fluxo de um campo elétrico por uma superfície fechada genérica é dada por
Na equação anterior, é a carga elétrica líquida dentro da superfície e um vetor unitário normal ao elemento infinitesimal de área . Esta superfície recebe o nome de superfície gaussiana.
A grande sacada de utilizar a lei de Gauss é que se tomarmos uma superfície gaussiana na qual o campo elétrico sobre ela possui módulo constante em todos os seus pontos, podemos retirar o módulo do campo elétrico da integral dupla anterior e isolá-lo.
A forma de escolher a superfície gaussiana se baseia na simetria do campo elétrico. Para o nosso caso, temos um fio infinito de carga. Assim, nosso campo elétrico tem simetria cilíndrica e a superfície gaussiana que utilizaremos é um cilindro.Agora que traçamos nossa estratégia, vamos aos cálculos!
Passo 2
Nessa passo vamos calcular o módulo do campo elétrico gerado pelo fio infinito. Vamos tomar como superfície gaussiana um cilindro de comprimento . Assim,
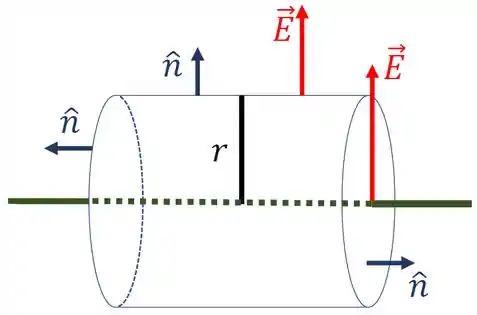
Assim, pela lei de Gauss, temos que
Na superfície gaussiana, o campo elétrico é perpendicular a lateral do cilindro e paralelo nas tampas. Deste modo, temos que
com a área da lateral do cilindro.
Assim, temos que
Vamos determinar a carga dentro da superfície gaussiana. Sabemos que o fio possui uma densidade linear de carga . Deste modo, temos imediatamente que
Já a área lateral é igual ao de um retângulo de base e altura . Logo,
Desta forma, finalmente temos que
Agora que determinamos o módulo do campo elétrico gerado pelo fio infinito, vamos para o próximo passo.
Passo 3
Sabemos que o módulo do campo elétrico gerado por uma carga pontual é
Mostramos no passo 2 que o módulo do campo elétrico gerado por um fio infinito é
O enunciado pede a distância na qual ambos os módulos dos campo elétricos sejam iguais. Assim,
Assim, quando , os módulos dos campos elétricos serão iguais.
Observando as alternativas, vemos que a alternativa correta é a letra .