(a)
(b)
(c)
(d)
(e)
Passo 1
Escrever a lei de Gauss e isolar a carga na equação:
Então, só resta calcular o fluxo.
Passo 2
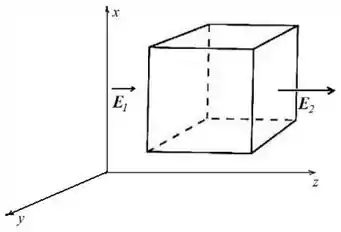
O fluxo nas superfícies de cima, de baixo, da frente e de trás são nulos, porque o campo não atravessa essas superfícies.
Só as partes da esquerda e da direita do cubo importam no problema e aí você tem que lembrar que quando o campo entra na superfície gaussiana o fluxo é negativo e quando o campo sai dela o fluxo é positivo. Por isso:
E, substituindo isso no passo :
Resposta
Letra (b).
Exercícios de Livros Relacionados
A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui