
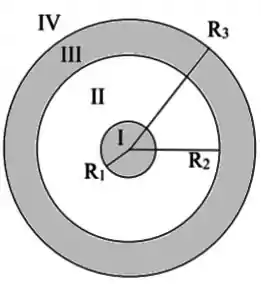
(a)
(b)
(c)
(d)
(e)
Passo 1
De cara, lembre-se do seguinte: dentro de condutores não temos campo elétrico. Então:
E a gente já elimina as letras (d) e (e).
Passo 2
Uma gaussiana esférica que envolve tudo, tanto a casca quanto a esfera dentro da casca, envolve uma carga total igual a:
Então, o fluxo elétrico é igual a zero e, como o campo é igual em todos os pontos dessa gaussiana esférica, temos que o campo fora da casca é igual a zero também.
E a gente já elimina as letras (b) e (c) e com isso já dá para marcar a letra (a) ;) mas, vamos continuar...
Passo 3
A carga dentro de uma gaussiana esférica na região só envolve a esfera menor, que tem uma carga igual a . Então:
O sentido é o mesmo de porque a carga da esfera menor é positiva e, logo, ela “cospe” o campo elétrico, para fora da esfera.
Além disso a questão diz que o vetor aponta justamente nesse sentido: saindo do centro e indo pro exterior da esfera.
Resposta
Letra (A)