A figura mostra as seções retas de duas placas de grande extensão, paralelas, não-condutoras, positivamente carregadas, ambas com distribuição superficial de cargas .
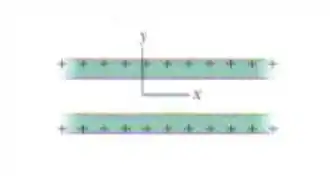
Determine o campo elétrico em termos dos vetores unitários.
(a) Acima das placas;
(b) Entre as placas;
(c) Abaixo das placas;
Passo 1
As duas placas infinitas geram campos elétricos uniformes com os módulos iguais. Isso ocorre porque a densidade superficial das duas é a mesma. Logo o módulo do campo gerado por cada placa é igual a:
Passo 2
O nosso problema se resume a olhar bem a direção dos vetores campo elétrico em cada região e procurar entender o que está acontecendo.
Sabemos que uma placa positiva gera um campo que sai dela.
Nas regiões que estão acima das duas placas e abaixo das duas placas, os campos estão no mesmo sentido, saindo das placas. Já na região entre as placas, os campos têm sentidos contrários e se anulam.
Assim:
Como o campo sai das placas positivas, na região acima das placas, o campo resultante aponta para cima e na região abaixo das placas, ele aponta para baixo.
Resposta
(a)
(b)
(c)