USP - Física 3 - Provas antigas - Prova de recuperação - 2022.1 - 3
Um cabo coaxial muito longo, de comprimento , é formado por um condutor cilíndrico de raio e por uma casca condutora cilíndrica de raio , conforme ilustrado na figura abaixo. Pelo condutor interno flui uma corrente I no sentido positivo de z positivo e pela casca externa flui uma corrente no sentido de negativo.
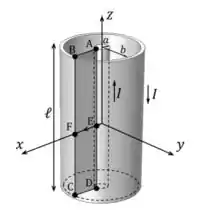
- Calcule o vetor campo magnético na região
- Calcule o fluxo do campo magnético na superfície delimitada pelos pontos ABCD, onde A = (), B = (), C = (), e D = (),
- Calcule ao longo do caminho aberto EF (com a orientação de E para F), onde E = () e F = ().
Passo 1
Salve gente bonita!!! Simbora resolver essa questão.
- Para descobrirmos o campo magnético na região desejada, vamos de acordo com os seguintes passos:
- Ver qual tipo de coordenada mais se enquadra na resolução de maneira que possa facilitá-la.
- Analisar se há simetria para que assim utilizemos um método mais fácil de resolver a questão.
- Utilizar o método e encontramos a resposta
- Gente, para essa letra, vamos utilizar a fórmula de se encontrar o fluxo do campo e resolver a integral, de maneira a deixarmos mais simples e no ponto de só substituir suas variáveis por valores caso fosse pedido.
- Galera, vamos tentar visualizar o que está acontecendo aqui. Temos dois vetores e .
Nesse caso, utilizaremos coordenadas esféricas, pois estamos trabalhando com um cilindro e as coordenadas esféricas se enquadra mais do que os outros dois tipos.
“Não entendi, my Lord”
Jovem gafanhoto, imagine uma esfera em um espaço tridimensional. Se você deixar e constantes, que objeto forma? Um cilindro!!
Por isso usamos as esféricas ( ͡~ ͜ʖ ͡°)
Por se tratar de um cilindro, temos simetria!! Então.... Qual fórmula podemos utilizar para descobrirmos o campo magnético??
A lei de Ampère. Assim, temos:
Como o campo elétrico é constante, sabemos que ele sairá de dentro da integral, sobrando apenas a integral de linha de . Se a imagem do cilindro é um círculo, será seu contorno. E qual o contorno de um círculo? Uma circunferência! Logo,
Passo 2
Observamos pela figura dada na questão que os quatro pontos formam um retângulo e sabemos que sua área é base vezes altura. A base, nesse caso, é a variação de , ou seja, , enquanto a altura é . Assim, .
Substituindo pela equação que achamos na letra A) e por, temos:
Utilizando propriedades de logaritmo, temos:
Passo 3
está na direção , enquanto está na direção . A imagem abaixo, vai facilitar essa visualização.
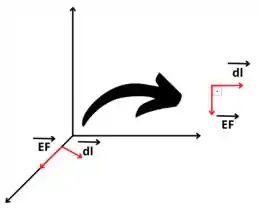
Como podemos ver, os vetores são perpendiculares, assim:
Pois no produto escalar é feito a multiplicação dos módulos dos vetores pelo cosseno do ângulo formado entre eles e o cosseno de 90° é zero
Resposta
Item
Item
Item C)