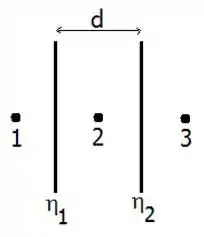
Suponha que você segure duas grandes folhas de plástico frente à frente, espaçadas uma da outra por , conforme mostra a figura. Atritando uma delas com lã e a outra com seda, você consegue obter, sobre a superfície de uma das folhas, uma densidade superficial uniforme de carga , e sobre a outra, outra densidade superficial uniforme de carga . Qual o vetor campo elétrico nos pontos , e ?
Passo 1
Para resolver essa questão vamos utilizar a Lei Gauss, como o campo obedece ao princípio da superposição, podemos lidar com cada folha separadamente. Vamos começar pela folha de densidade !
Para planos carregamos, é comum usarmos a gaussiana em forma de prisma, pois dessa forma, apenas o fluxo das tampas contribui, temos então:
Considerando que temos um prisma, a área das duas tampas será , para a carga interna, temos que a carga será a densidade superficial multiplicada pela área que está dentro da nossa gaussiana, ou seja . Substituindo, temos:
O sinal de menos nos mostra que o campo vai sempre em direção à folha, ou seja, na região , ele aponta para a direita, e nas regiões e , ele aponta para a esquerda.
Veremos agora o campo produzido pela folha de densidade !
Passo 2
Para essa folha, vamos utilizar o mesmo processo do item anterior, pela Lei de Gauss, temos:
O sinal positivo nos diz que o campo aponta sempre para fora da folha carregada, ou seja, nas regiões e ele aponta para a esquerda, e na região ele aponta para a direita.
Pronto, analisando os dois resultados, vemos que o campo será nulo nas regiões e , e na região , entre as placas, valerá:
Para escrever o vetor campo elétrico resultante em cada região, iremos utilizar o sistema de coordenadas usual:
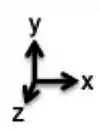
Como o campo aponta perpendicularmente à folha, temos: