A figura ao lado ilustra uma esfera oca condutora de raio interno e raio externo , que tem uma carga elétrica negativa . Uma carga pontual positiva é fixada no centro da esfera oca. Na figura, representa uma distância radial qualquer ao centro da esfera. Existe vácuo nas regiões e .
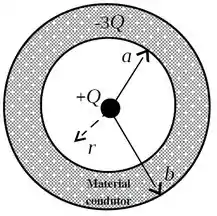
(a) Calcule o vetor campo elétrico (módulo, direção e sentido) em todos os pontos do espaço, ou seja, nas regiões (i) , (ii) e (iii) .
(b) Represente, em um desenho esquemático, um esboço das linhas de campo elétrico nas regiões , e .
(c) Determine a densidade superficial de carga na (i) superfície interna da esfera oca () e na (ii) superfície externa da esfera oca ().
Passo 1
Vamos resolver apenas os itens (a) e (b) dessa vez, beleza?
Bem, vamos inicialmente analisar o problema: se temos uma carga positiva no interior de uma casca condutora, a carga positiva irá induzir uma carga negativa na superfície da casca interna, certo? A superfície da casca externa vai ficar então com os restantes.
A figura abaixo mostra o que acontece.
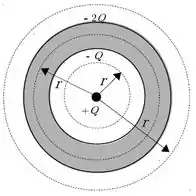
Passo 2
Agora, vamos utilizar a Lei de Gauss para calcular o vetor campo elétrico em cada uma das três regiões pedidas no enunciado, ou seja,
Em todas as três regiões, o vetor é paralelo ao vetor normal da superfície. Temos, então, do lado direito da equação acima:
Isso simplifica a equação da Lei da Gauss para a seguinte expressão:
Passo 3
Para a região (i) , a carga interna é a carga pontual . Fazemos a substituição direta na expressão simplificada obtida no Passo 2:
O vetor campo elétrico para essa região é dado por:
onde é o vetor unitário que aponta para fora da carga positiva.
Passo 4
Para a região (ii) , a carga interna é nula, já que é uma casca esférica condutora! Com , .
Passo 5
Para a região (iii) , a carga interna é a soma da carga pontual com a carga da casca esférica , ou seja, . Fazemos a substituição direta na expressão simplificada obtida no Passo 2:
O vetor campo elétrico para essa região é dado por:
Passo 6
Bem, para desenhar um esboço das linhas de campo elétrico, precisamos lembrar que o campo sai das cargas positivas e entra nas negativas, o que está de acordo com a resposta obtida no item (a)!
As linhas de campo elétrico estão esboçadas na figura abaixo.
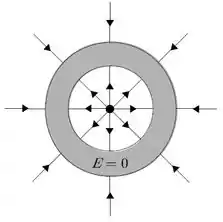
Resposta
(a) O vetor campo elétrico para as três regiões é dado por:
- Região : ;
- Região : ; e
- Região : .
(b) As linhas de campo elétrico são esboçadas na figura do Passo 6.