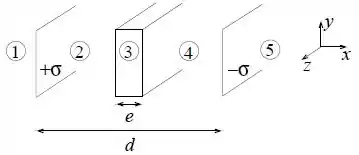
Considere duas placas grandes, paralelas, a uma distância uma da outra, uma delas com densidade superficial de carga , uniforme, e a outra com densidade . Entre as duas placas paralelas é colocada uma chapa metálica de espessura , conforme mostra a figura.
Demonstre que a intensidade do campo elétrico criado por um plano infinito com densidade superficial de carga é .
Utilizando o princípio de superposição e desprezando efeitos de borda, determine o vetor campo elétrico nas regiões e .
Se a chapa metálica for retirada da região entre as placas, haverá aumento ou diminuição da energia eletrostática do sistema? Justifique a resposta.
Passo 1
Demonstre que a intensidade do campo elétrico criado por um plano infinito com densidade superficial de carga é .
Esse é um problema clássico de Lei de Gauss, que é dada por:
Para calcular o campo elétrico criado por um plano infinito, vamos usar como gaussiana um cilindro de área transversal que engloba apenas parte da placa infinita de carga , como mostra a imagem:
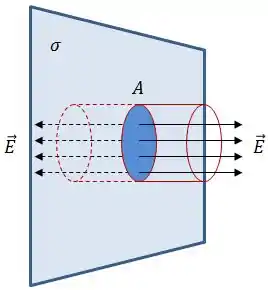
Assim, podemos dar uma simplificada na Lei de Gauss:
O termo aparece pois o campo elétrico atravessa a gaussiana tanto na área da direita quanto na área da esquerda.
Onde é a densidade superficial de carga.
Passo 2
Utilizando o princípio de superposição e desprezando efeitos de borda, determine o vetor campo elétrico nas regiões e .
Em cada região, o campo elétrico resultante será a soma vetorial dos campos elétricos gerados por cada placa. Então, pra não nos enrolarmos, é uma boa darmos nomes às placas.
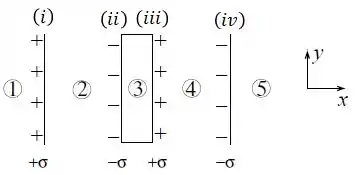
Agora é só calcular o campo elétrico para cada região. Em cada uma delas:
Passo 3
- Região 1
- Região 2
- Região 3
- Região 4
- Região 5
Passo 4
Se a chapa metálica for retirada da região entre as placas, haverá aumento ou diminuição da energia eletrostática do sistema? Justifique a resposta.
A densidade de energia eletrostática é dada por:
E a energia eletrostática é dada por:
Assim, quando retiramos a chapa metálica, acabamos aumentando o volume onde o campo elétrico não é nulo, já que o campo elétrico no interior da placa (Região 3) é nulo.
Portanto, haverá aumento da energia eletrostática.
Resposta
Haverá aumento da energia eletrostática.