A figura mostra, em seção reta, duas esferas de raio , com distribuições volumétricas uniformes das cargas. O ponto está sobre a reta que liga os centros das esferas, a uma distância do centro da esfera . Se o campo elétrico no ponto é igual a zero, qual é a razão entre a carga da esfera e a carga da esfera ?
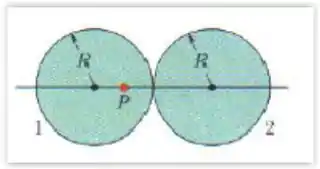
Passo 1
Encontrar o campo elétrico que a esfera exerce em . Nesse caso, o campo aponta no sentido da esquerda, supondo que as cargas das esferas são positivas. A lei de Gauss em simetria esférica nos leva sempre à mesma conclusão:
é a distância do centro da esfera até o ponto , que vale, no problema, . Então:
Passo 2
Só que é a carga que está dentro de uma esfera menor, de raio , afinal, é esta a gaussiana que utilizaríamos para calcular o campo elétrico no ponto , localizado dentro no interior da primeira esfera.
Para calcular , vamos usar a informação de que as esferas são uniformemente carregadas. A densidade volumétrica da primeira esfera vale:
Logo:
Substituindo na equação do passo anterior:
Passo 3
O mesmo cálculo é realizado para o caso da esfera :
Porém, com duas diferenças:
- A distância vale:
- A carga interna se encontra dentro de uma gaussiana que envolve toda a esfera . Então, nesse caso,
Logo:
Passo 4
Para que as duas forças se anulem, o módulo delas deverá ser o mesmo e, com isso, podemos encontrar a razão entre as cargas: