Considere uma esfera isolante de raio carregada com a densidade volumar de carga , sendo uma constante e a distância de um ponto genérico ao centro da esfera. Considere também uma barra de comprimento e densidade linear de carga constante . A barra está orientada para o centro da esfera e o seu ponto médio está a uma distância do centro da esfera, sendo , como mostrada na figura abaixo.
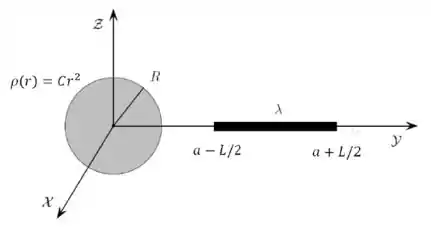
- Determine a carga da esfera.
- Utilizando a lei de Gauss, calcule o campo eletrostático (módulo, direção e sentido) produzido apenas pela esfera, num ponto , situado a uma distância do centro da esfera, tal que .
- Calcule a força eletrostática (módulo, direção e sentido) exercida pela esfera sobre a haste.
- Obtenha uma expressão aproximada para a força exercida pela esfera sobre a haste para e discuta o resultado encontrado.
Passo 1
a) Como a distribuição de cargas no volume da esfera não é uniforme, precisamos realizar a seguinte integral para obter o valor da carga total no volume da esfera isolante
em que é o elemento infinitesimal de volume esférico.
Para entender como é calculado o elemento de volume neste caso, considere a figura abaixo.
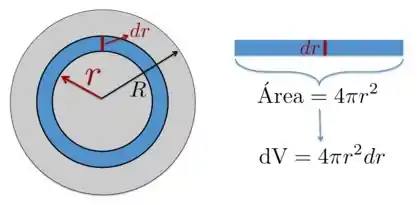
Nessa figura, temos um volume esférico infinitesimal em azul, representado esquematicamente à direita da figura, cuja área da base é igual a de uma superfície de uma esfera de raio : . Essa é apenas uma figura para ajudar você a se lembrar de como é o elemento de volume esférico. Para termos , precisamos multiplicar essa “área da base” pela “altura” .
Portanto, o elemento de volume é dado por
Se substituímos as expressões de dado na questão e a de acima para o elemento de volume na expressão para a carga total , chegamos a
Com isso, vemos que a constante pode ser escrita como
Passo 2
b) Como o problema tem simetria esférica, podemos utilizar a lei de Gauss para determinar o valor campo elétrico em uma posição . Considerando uma esfera de raio envolvendo toda a carga , em cada ponto sobre a superfície dessa esfera de raio o campo elétrico é radial, ou seja, seu vetor está na direção do raio da esfera.
Se consideramos agora o elemento de área da superfície gaussiana paralelo a , a integral na lei de Gauss é simplificada para
Uma outra característica importante dessa simetria esférica é que o campo elétrico sobre cada ponto da superfície gaussiana esférica tem o mesmo valor. Por isso, na expressão acima, podemos retirar da integral, o que nos conduzirá à
Com isso, o vetor campo elétrico é dado por
Note que esse resultado nos diz que o campo elétrico produzido pela carga distribuída pelo volume do isolante é idêntico àquele campo produzido caso a carga estivesse toda concentrada no ponto central da esfera. Esse resultado nos auxilia no cálculo da força elétrica do próximo item.
Passo 3
c) O resultado do item anterior nos mostrou que podemos considerar a carga total da esfera como se estivesse toda concentrada em seu centro, como representado na figura abaixo. Por isso, o campo elétrico na posição pode ser obtido da expressão para o campo que obtivemos no item b) e está representado na figura.
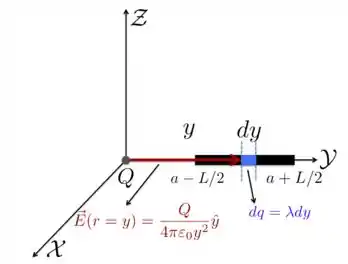
Como o campo produzido pela carga da esfera isolante é radial, a força infinitesimal que o campo exerce sobre uma carga infinitesimal do fio é dada por
Para sabermos o valor da força total sobre a barra, precisamos integrar de a ,
Simplificando essa expressão, temos
Passo 4
- Note que podemos reescrever a expressão acima como
Agora, se , então temos que
e a força é, após essa simplificação, fica
Como é a carga total da haste de comprimento ,
Repara, galera, que para resolvermos todos os itens não precisamos, em momento algum, dizer se as cargas da esfera e da barra são positivas ou negativas. Da expressão acima para a força, vemos que a sua direção estão bem definida: . Porém, o sentido da força vai depender dos sinais das cargas e .
Concluindo, se , podemos considerar a força entre a esfera e a barra como se fosse uma força entre duas cargas e puntiformes separadas por uma distância , com a carga da esfera toda concentrada na origem e a da barra toda concentrada em seu ponto médio.
Resposta
- .
c) .
d)