Uma seção de comprimento do cilindro infinito de raio , mostrado na Figura 1, tem carga total . Esta carga se distribui no volume definido pela seção de acordo com densidade volumétrica de carga . A densidade não varia ao longo do eixo do cilindro, o que permite definir a densidade linear de carga . Determine a relação entre e , considerando os valores de e conhecidos.
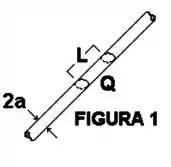
Determine o módulo do vetor campo elétrico em um ponto qualquer afastado da distância (onde do eixo do cilindro infinito (Figura 1), considerando o valor de conhecido.
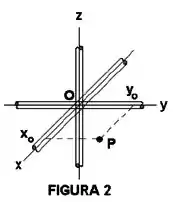
Três cilindros idênticos (raio e densidade linear de carga ) estão alinhados com os eixos coordenados, conforme mostra a Figura 2. Determine o vetor campo elétrico em um ponto de coordenadas situado no plano e fora dos três cilindros, desprezando as distorções devidas à junção situada em torno da origem.
Passo 1
A carga total do volume do cilindro pode ser calculada por meio de uma integral, tripla, chato, eu sei! Mas nem é tão difícil, se liga!
Lembrando que cara coordenadas cilíndricas, :
Como :
Passo 2
Para determinar o campo produzido, vamos usar a linda Lady Gauss. Usaremos uma gaussiana cilíndrica, lembrando que, nesse caso, o campo é sempre paralelo ao vetor área, logo:
O vetor campo aponta sempre na direção radial!
Passo 3
Para determinar o campo no ponto , podemos calcular o campo produzido por cada fico em separado e depois somar cada campo vetorialmente.
Vamos começar calculando o campo produzido pelo fio que está sobre o eixo . O ponto está a uma distância do fio e o campo irá apontar na direção positiva do eixo , logo:
Analogamente, o ponto está a uma distância do fio que se encontra sobre o eixo , e campo apontará na direção positiva do eixo , logo:
Para o fio que está sobre o eixo , complica um pouquinho, mas nem tanto, agora, o campo terá uma componente em e uma em , e o ponto está a uma distância do fio. As componentes serão:
Onde e , logo:
Somando todas as componentes do campo, temos:
Resposta