Considere duas grandes placas planas, paralelas. Uma das placas com uma densidade de cargas se encontra na origem do eixo e a outra, com está localizada em .
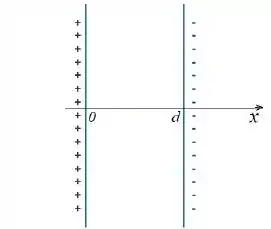
Qual é o vetor campo elétrico no ponto médio se o eixo passa pelo centro das duas placas? (considere que as dimensões das placas são muito maiores que a distância entre elas)
Passo 1
Os módulos dos campos gerados pelas placas positiva e negativa são, respectivamente:
As linhas de campo saem da placa positiva e entram na placa negativa, de forma que, na região entre as duas placas, os campos possuem a mesma direção e sentido .
Como resultado, o campo resultante nessa região será a soma dos dois campos:
Finalmente, o vetor campo resultante na região entre as placas será:
Resposta
Exercícios de Livros Relacionados
A Fig. 23-30 mostra uma superfície gaussiana com a forma de um cubo de 2,00 m de aresta, imersa em um campo elétrico dado porE → = 3,00 x + 4,00 i ^ + 6,00 j ^ + 7,00 k ^ N / C , com x em metros. Qual
Uma fina casca esférica não-condutora de raio R 1 tem carga total q 1 uniformemente distribuída em sua superfície. Uma segunda fina casca esférica não condutora e maior, de raio R 2 , coaxial com a pr
Uma esfera de raio R tem densidade volumétrica de carga ρ = B / r para rR , onde B é uma constante e ρ = 0 para rR . (a) Determine a carga total na esfera. (b) Determine as expressões par ao campo elé
Um cilindro sólido não condutor infinitamente longo de raio a tem uma massa específica volumétrico uniforme de ρ 0 . Mostre que o campo elétrico é dado pelas seguintes expressões: E R = ρ R / 2 ε 0 pa
Uma fina casca cilíndrica de comprimento 200m e raio 6,00c m tem uma densidade superificial uniforme de carga de 9,00n C / m 2 . (a) Qual é a carga total na casca? Determine o campo elétrico nas segui