Um cilindro maciço muito longo, não condutor, de raio e comprimento , contém uma densidade volumétrica de carga , uniforme.
Considere a distância ao eixo do cilindro. Desprezando efeitos de borda, determine:
a carga total do cilindro em função de , e ;
o módulo do campo elétrico para ;
o módulo do campo elétrico para .
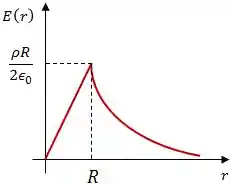
Esboce o gráfico do módulo do campo elétrico em função de . Indique no gráfico o raio do cilindro.
Passo 1
a carga total do cilindro em função de , e ;
Por definição, a carga do cilindro e a densidade volumétrica de carga estão associadas por:
Como , teremos:
Passo 2
o módulo do campo elétrico para ;
Aplicando a Lei de Gauss à simetria cilíndrica, teremos:
Onde é o raio da seção transversal da nossa gaussiana cilíndrica.
Assim, basta, para cada caso, calcular o valor da carga interna à gaussiana.
Passo 3
Para , a gaussiana cilíndrica engloba todo o cilindro, logo:
Aplicando isso à expressão que encontramos no Passo 2, teremos:
Passo 4
o módulo do campo elétrico para .
Nesse caso, a gaussiana engloba apenas parte do cilindro, logo:
Logo, o campo elétrico será dado por:
Passo 5
Esboce o gráfico do módulo do campo elétrico em função de . Indique no gráfico o raio do cilindro.
Juntando os resultados das letras e , teremos:
É importante notar que, quando , ambos valem:
Logo, a função não possui descontinuidades.
Por fim, o gráfico vai ter essa cara:
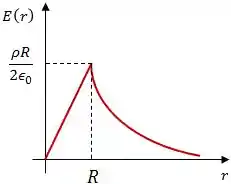
Resposta