Um cilindro maciço infinito, não condutor, de raio , apresenta uma densidade volumétrica de carga variável dada por , onde é uma constante positiva e é a distância ao eixo de simetria do cilindro.
Considere duas superfícies gaussianas cilíndricas (figura abaixo) e (figura abaixo), com mesmo eixo de simetria do cilindro maciço, alturas , raios e , respectivamente.
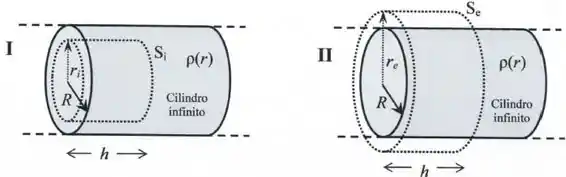
Note que suas respostas podem conter apenas as variáveis , , , , e .
Calcule a carga elétrica no interior de e a carga elétrica contida no interior de .
Calcule o módulo do campo elétrico , para e para .
Esboce um gráfico de em função de , considerando as regiões e .
Passo 1
Calcule a carga elétrica no interior de e a carga elétrica contida no interior de .
Vamos começar entendendo como calcular a carga elétrica nessas situações.
A densidade volumétrica de carga é definida por:
Assim, se quisermos calcular a carga em determinada região, basta fazer:
Nesse caso, como se trata de uma superfície cilíndrica, o elemento será:
Além disso, o enunciado nos disse que a densidade volumétrica de carga é dada por:
Substituindo na expressão acima, teremos:
Agora basta aplicar isso para cada situação.
Passo 2
No interior de , o raio varia entre e , logo:
Já no interior de , como , o raio da nossa integral irá variar apenas entre e . Logo:
Passo 3
Calcule o módulo do campo elétrico , para e para .
O campo elétrico pode ser calculado utilizando a Lei de Gauss, dada por:
Como estamos trabalhando com simetria cilíndrica, teremos:
Agora basta aplicar isso a cada caso.
Nesse caso, , logo:
Substituindo a expressão de , teremos:
Nesse caso, , logo:
Substituindo a expressão de , teremos:
Passo 4
Esboce um gráfico de em função de , considerando as regiões e .
Quando , temos o caso de , onde o campo elétrico varia quadraticamente, de acordo com a equação:
Para , temos o caso de , onde módulo do campo passa a decair de acordo com a equação:
Assim, o gráfico terá essa cara:
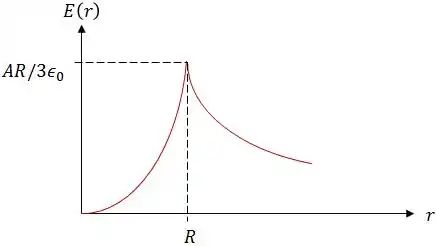
Resposta