UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille – Segunda Lista de Exercícios, Questão 16c
Esboce cada curva parametrizada a seguir e determine seu comprimento.
(c) A catenária com . Lembre-se:
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma curva parametrizada por com e nós precisamos determinar o comprimento dela e esboçar a curva no gráfico.
O comprimento de uma curva parametrizada é definida da mesma forma que o comprimento de uma curva plana com equações paramétricas. Se a curva é percorrida exatamente uma vez, à medida que cresce de para , seu comprimento é determinado pela equação:
No nosso caso, o intervalo é dado por . Além disso, nossas componentes no vetor nos dão e . Derivando e em relação a , elevando ao quadrado, somando os dois resultados e calculando a raiz quadrada, vamos conseguir calcular a integral do comprimento de arco definida por .
Vamos lá!
Passo 2
Galera, o integrando pode ser escrito de maneira mais compacta como o módulo do vetor , ou seja:
Então, vamos começar calculando esse módulo. Para e , temos as derivadas:
Colocando a na fórmula do módulo:
Elevando as componentes ao quadrado:
Usando a identidade trigonométrica , temos:
Tirando da raiz:
E ficou bem mais simples de integrar, né? Então, vamos lá.
Passo 3
Substituindo o valor que encontramos para na nossa integral, temos:
Lembrando que , vamos ter:
Integrando a nossa função:
Aplicando os limites de integração, temos nosso comprimento :
Plotando nossa trajetória no plano cartesiano e no espaço tridimensional, temos:
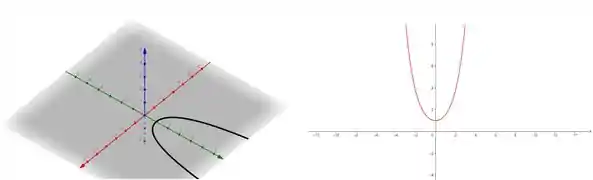
Prontinho, galera! Até a próxima! 😉