Seja a curva com equações paramétricas
Esboce a curva
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 2. Dessa vez estaremos trabalhando curvas parametrizadas.
Nosso objetivo é desenhar a curva parametrizada como

Passo 2
Para desenhar a curva, vamos obter suas equações cartesianas. Como
Vamos isolar
logo,
Substituindo esse valor em .
Dessa forma, temos que
Ou seja, nossa equação cartesiana é uma exponencial
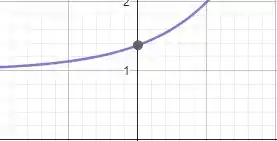

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento Acima