Uma partícula se desloca ao longo de uma curva descrita por:
Encontre a equação para uma superfície quádrica que contenha a curv. Identifique a quádrica.
Passo 1
Essa questão pode ser muito simples se você conseguir enxergar isso que vou te mostrar agora:
Observe a relação
Observe ainda que
Passo 2
Então sabemos que realmente é parametrizado por:
Então a curva que procuramos está contida na superfície
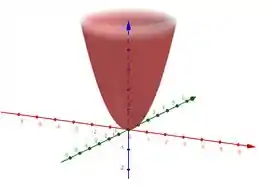
Resposta
Ei, a resposta está no passo a passo :)