UFSC, Sem Campus, Cálculo C, Provas Professor Saeger - P2 2022.1, Questão 1
1 – Parametrize a curva C definida por
E esboce duas de suas projeções nos planos coordenados.
Passo 1
Fala aí, querido!! Tudo certinho? Bora resolver esse probleminha? 😉
Nesse problema temos que parametrizar a curva definida por partes e projetar duas curvas nos planos coordenados.
Parece complicado? 🤔
Para parametrizar uma curva, definimos uma variável como principal e definimos as outras variáveis em função da variável principal.
Sacou? Bora começar! 😬
Passo 2
Vamos definir como nossa variável principal e fazer .
Dessa forma podemos escrever como
Já para , temos
Portanto pode ser parametrizado como
Tranquilo até aqui? 😉
Passo 3
Para esboçar as projeções de nos planos coordenados, escolhemos duas coordenadas entre e igualamos à variável do plano escolhido, por exemplo
Esboçando essas equações cada uma em seu plano, temos
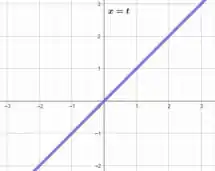
Sacou como faz? Responde Aí! 😉