UFRJ, Sem Campus, Cálculo 2, Listas de Cálculo 2 - UFRJ - Lista de Curvas Parametrizadas, Questão 8b
Suponha que a posição de duas partículas no instante t seja dada por ,
, respectivamente.
Trace as trajetórias de ambas as partículas;
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 2. Dessa vez estaremos trabalhando curvas parametrizadas.
Nosso objetivo é traçar as trajetórias de ambas as partículas;
,, respectivamente.
Passo 2
Bem, na questão anterior já descobrimos as equações cartesianas das trajetórias. Elas são
Desenhando a hipérbole e a elipse, temos:
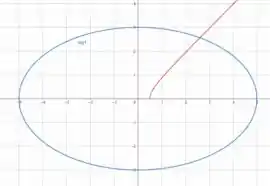
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento Acima
Exercícios de Livros Relacionados
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.d) r → t = 2 cos 3 t ,2 s e n 3 t , t ∈ 0 , π 2
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.b) r → t = t ,t + 2 ,4 - 2 t , t ∈ 0 ,1
Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.a) r → t = 2 + 3 cos t ,1 + 4 s e n t , t ∈ 0 ,2 π