Exercícios Resolvidos de Parametrizações Clássicas

Exercício 51 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89

Enunciado

UFRJ, Sem Campus, Cálculo 2, Listas de Cálculo 2 - UFRJ - Lista de Curvas Parametrizadas, Questão 3c

Escreva a equação cartesiana da curva e faça um esboço indicando a direção na qual a

curva é traçada quando o parâmetro aumenta.

Passo 1

Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 2. Dessa vez estaremos trabalhando curvas parametrizadas.

Nosso objetivo é desenhar a curva parametrizada

dizer sua equação no plano cartesiano e a direção no qual a curva é traçada quando o parâmetro aumenta.

Passo 2

Vamos começar a obter a equação cartesiana. Como

Temos que

Logo,

Ou seja, nossa equação cartesiana é uma exponencial

com

Esboçando a curva

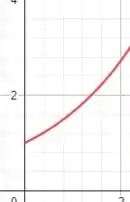
Quanto ao seu sentido, como é crescente em . O sentido é de crescimento da coordenada .

Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊

Resposta

Desenvolvimento Acima

Exercícios de Livros Relacionados

Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.

Para cada um dos seguintes pares de equações paramétricas, esboce a curva e determine a sua equação cartesiana.

Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.d) r → t = 2 cos 3 ⁡ t ,2 s e n 3 t , t ∈ 0 , π 2

Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.b) r → t = t ,t + 2 ,4 - 2 t , t ∈ 0 ,1

Esboçar as curvas seguintes, representando o sentido positivo de percurso. Obter uma parametrização da curva dada, orientada no sentido contrário.a) r → t = 2 + 3 cos ⁡ t ,1 + 4 s e n t , t ∈ 0 ,2 π