UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille – Segunda Lista de Exercícios, Questão 15d
Considere a espiral , , e a circunferência de equação .
(d) Desenhe a trajetória de e a circunferência , destacando a interseção entre elas.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma curva parametrizada por e uma circunferência de equação . Nós precisamos plotas essas duas curvas no gráfico cartesiano.
A gente pode pensar em como sendo o movimento de uma partícula sendo descrito em cada instante . Então, é um vetor posição do ponto na curva, suas equações paramétricas são:
Então, a gente percebe que a trajetória é descrita somente no plano . Em , temos e , isso significa que a trajetória começa na origem e percorre a curva de movimento até encontrar a circunferência no ponto de interseção.
Dessa forma, vamos verificar onde as curvas se interceptam e desenhar a trajetória de com a ajuda de um software, para ter mais precisão.
Vamos lá!
Passo 2
Definidas as componentes do vetor em termos de e no passo anterior, podemos substituir os valores de e na equação da circunferência:
Elevando ao quadrado:
Colocando em evidência:
Usando a identidade trigonométrica , temos:
Como , isolando temos:
Logo,
Passo 3
Isso significa que em a trajetória encontra a circunferência . No espaço tridimensional, temos um cilindro circular reto (mostrado em vermelho) e a trajetória plotada com variando de a na figura:
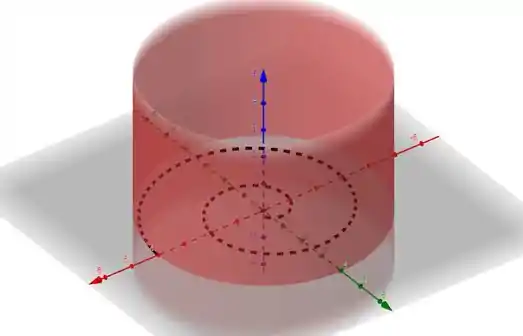
Onde descreve uma trajetória em espiral no plano , como mostrado.
Prontinho, galera! Até a próxima! 😉