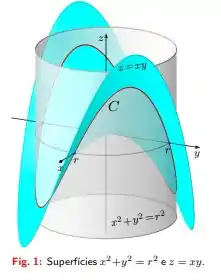
Seja a curva fechada dada pela interseção das superfícies de equações cartesianas e (Fig. 1).
Dê equações paramétricas para a reta tangente a no ponto .
Passo 1
Eaew, tudo certinho contigo?
Temos uma curva obtida pela interseção entre as superfícies e , a interseção ocorre como na figura
Temos que encontrar uma parametrização para a reta tangente a curva no ponto , a reta tangente é aquela na qual a inclinação é dada pela derivada da curva no ponto! Ou seja
em que em nosso caso, um ponto que pertence a reta! Na alternativa anterior obtemos que a parametrização da curva é dada por
Vamos calcular então a nossa derivada! Saca só!
Passo 2
A derivada em relação a é dada por
Temos aqui duas derivadas conhecidas como
e
para a outra derivada precisamos usar a regra do produto para obter
usando as derivadas que acabei de apresentar, temos que
a derivada da curva pode ser escrita como
Vamos usar essa expressão para calcular a nossa equação da reta tangente!
Passo 3
Precisamos avaliar a expressão no ponto desejado! , portanto, temos que
temos que e , isso é verdade para , portanto, temos que
e, a equação da reta tangente é dada por
A segunda alternativa já era! Te vejo na próxima!