UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille – Segunda Lista de Exercícios, Questão 17a
Uma partícula se move no plano segundo o vetor posição .
(a) Verifique que a trajetória está sobre a parábola e desenhe a trajetória.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu uma curva parametrizada por e uma parábola de equação . Nós precisamos determinar se essa curva está sobre a parábola.
Para isso, vamos verificar se as componentes do vetor satisfazem a equação da parábola. Essas componentes são:
Substituindo em , vamos verificar se a trajetória da curva está sobre a parábola.
Vamos lá!
Passo 2
Vamos começar substituindo e em :
Fazendo o produto dos termos:
Usando a fórmula do arco duplo, , temos:
Simplificando, vamos obter:
Portanto, nossa curva paramétrica satisfaz a equação da parábola e podemos dizer que a curva está sobre a parábola. Esse fato é verificado observando o gráfico das duas na figura abaixo:
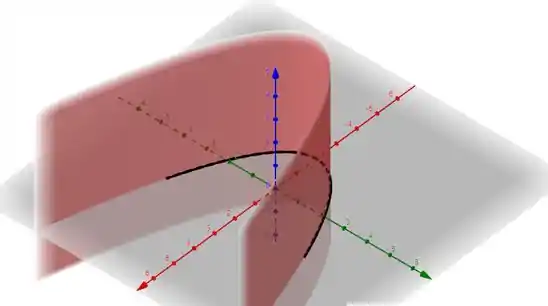
Prontinho, galera! Até a próxima! 😉