UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille – Segunda Lista de Exercícios, Questão 11
Considere o cilindro circular reto e o plano . Obtenha uma parametrização para a curva correspondente à interseção e esboce, em uma mesma figura, o cilindro e o plano , destacando a trajetória da curva .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu um cilindro circular reto, de equação , e um plano definido pela equação . Nós precisamos obter uma parametrização para a curva na interseção dessas superfícies.
Para isso, depois de identificadas as equações das superfícies, nós vamos isolar uma variável de uma das equações, substituir essa variável na outra equação e parametrizar a equação, chamando uma das variáveis de . Vai ficar mais claro a medida que a gente for fazendo.
Vamos lá!
Passo 2
Nós temos as equações das duas superfícies:
Isolando na primeira equação, temos:
Substituindo esse valor de na equação do plano, , temos:
Isolando , vamos deixar a equação apenas em função de :
Agora, para parametrizar a equação, nós podemos chamar . Assim:
E como a gente definiu lá em cima, , com vamos ter:
Dessa forma, temos nossa curva parametrizada:
Galera, presta atenção no sinal da raíz na hora de plotar a curva, tá? Porque nós temos sempre uma raiz positiva e uma negativa, então é como se tivéssemos dois vetores, um e um , beleza? Isso vai fazer a curva em preto ficar completinha, como mostra a figura abaixo:
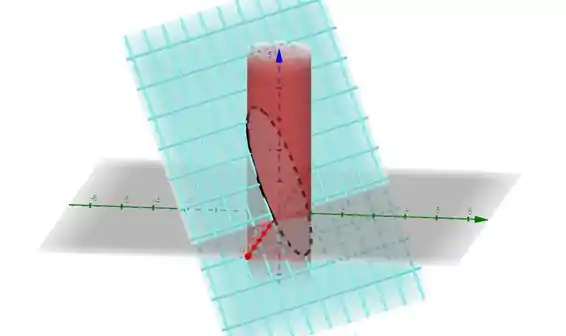
Com a ajuda de um software basta inserir a equação do cilindro circular reto (em vermelho), , e a equação do plano (em azul claro), . A curva em preto representa a parametrização da interseção entre as superfícies.
Valeu, galera! Até a próxima! 😉