UFRJ, Sem Campus, Cálculo 2, Listas de Cálculo 2 - UFRJ - Lista de Curvas Parametrizadas, Questão 5
Seja P um ponto a uma distância do centro de uma roda de raio , que gira sem deslizar
sobre o eixo . Reproduzindo o esquema que usamos para parametrizar a ciclóide (caso
em que ), mostre que a curva descrita pelo ponto , chamada trocóide, tem equações
paramétricas
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 2. Dessa vez estaremos trabalhando curvas parametrizadas.
Nosso objetivo é determinar uma parametrização para a trocóide, e mostrar que uma parametrização é dada por
Passo 2
Antes de fazer a parametrização da trocóide, vamos relembrar a parametrização da ciclóide. Para isso vamos observar o desenho a seguir.
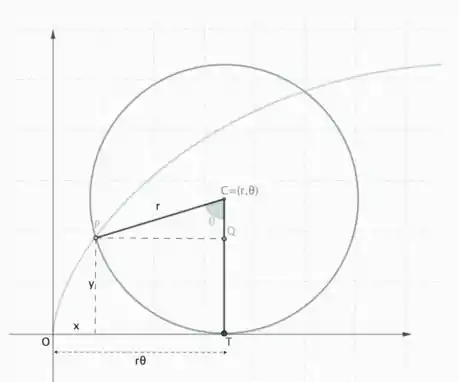
Vamos parametrizar a ciclóide com os parâmetros . Note que quando a circunferência rola graus ela percorre de distância, dessa forma podemos observar as seguintes relações
Temos que as coordenadas do ponto são dadas por
Passo 3
Agora vamos pensar no caso da trocóide. Como nosso ponto está dentro da circunferência, vamos representar a situação da seguinte forma.
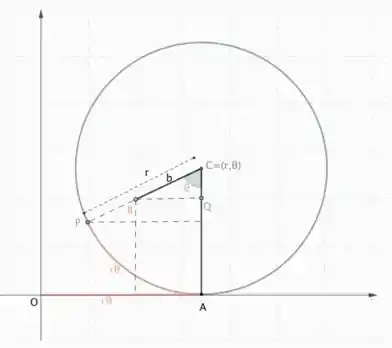
Ou seja, é bem parecido com o caso da ciclóide. Vamos encontrar a coordenada do nosso ponto . Suas coordenadas e são
Ou seja, é bem parecido com a ciclóide.
Dessa forma, provamos que a parametrização da trocóide é
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento Acima