USP, Sem Campus, Cálculo 2, Listas de Cálculo 2 - USP, Politécnica - Lista 2 - Várias Variáveis, Limites e Continuidade, Questão 1.5a
1.5. Seja , para .
a. Desenhe a imagem de , indicando o sentido de percurso.
Passo 1
Iae, meus queridos! Está com dificuldades nessa questão? Não se preocupe! Estamos aqui para ajudar 😉
Nesse problema queremos obter o gráfico da função parametrizada .
E agora? O que a gente faz? 👀
Para esboçar uma curva parametrizada do tipo , pegamos a primeira função e igualamos a e a segunda a , ou seja
Na primeira equação, isolamos e substituímos na em , assim vamos obter uma curva .
Já para descobrir o sentido da curva, pegamos um ponto de e calculamos e outro ponto em fazendo de modo que , assim, vemos que a função vai de para .
Bora ver tudo isso na prática! 😉
Passo 2
A função é dada por
Igualando a primeira componente a e a segunda a , temos
Isolando na primeira equação, vamos obter
Substituindo essa equação em , vamos obter
Portanto, essa é a nossa função que vamos esboçar o gráfico!
Tranquilo até aqui? 😎
Passo 3
Agora vamos ver qual o sentido dessa curva...
Vamos usar e
A curva caminha de para , portanto esboçando a curva
E os pontos e , vamos obter
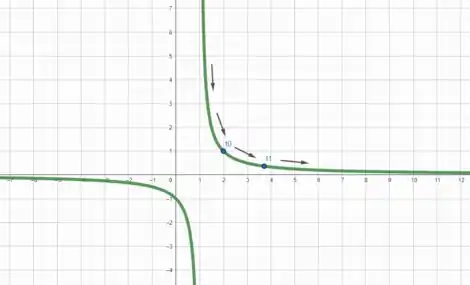
É isso, espero ter ajudado! Entendeu tudo? Responde Aí! 😎👍
Resposta
