UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille – Segunda Lista de Exercícios, Questão 12
Seja a função . Verifique que parametriza a curva interseção das superfícies e . Que superfícies são essas? Esboce-as e destaque a trajetória de . Destaque os pontos .
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu duas superfícies, e , e uma curva que parametriza a interseção dessas superfícies. Para verificar se essa é mesmo uma parametrização, basta a gente usar as componentes do vetor na forma cartesiana:
Substituindo , e nas equações das superfícies, nós vamos verificar as igualdades para saber se a curva parametriza as equações. Em seguida, vamos identificar e esboçar cada superfície junto com os pontos .
Vamos lá!
Passo 2
Vamos começar verificando as equações paramétricas , e . Substituindo na equação , temos:
Então, satisfaz a equação. Agora vamos testar em . Substituindo as equações paramétricas, temos:
Simplificando, temos também:
Portanto, podemos dizer que é uma parametrização para a interseção das superfícies e . Outra forma de verificar, seria plotando a curva junto com as superfícies. É que nós vamos fazer agora.
Passo 3
Repare que em , é como se tivéssemos duas parábolas, e , rotacionando em torno do eixo . Então, essa superfície é chamada de paraboloide de revolução, que é como um copo de forma oval:
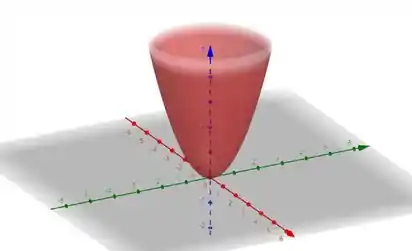
E em , nós temos um plano:
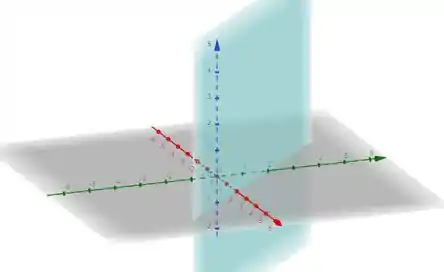
Juntando as duas superfícies com , temos a curva de interseção das superfícies, representada no nosso gráfico em preto:
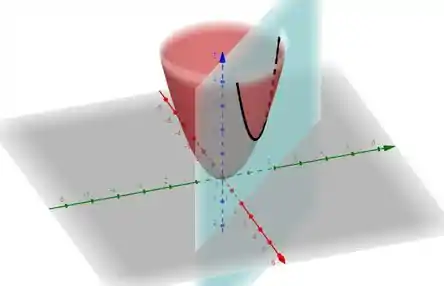
Agora para encontrar os pontos , vamos substituir os valores referentes de em :
Nó gráfico, eles são representados pelos pontos , e :
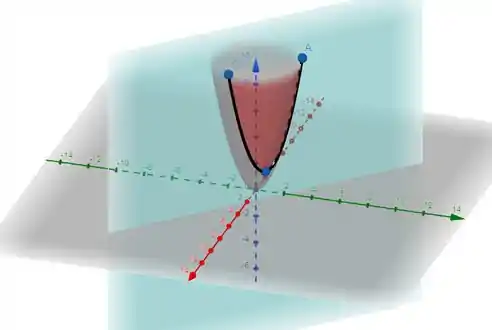
Prontinho, galera! Até a próxima! 😉