UFU, Sem Campus, Cálculo 2, Listas de Cálculo 2 - Profº M. C. Fenille – Segunda Lista de Exercícios, Questão 17b
Uma partícula se move no plano segundo o vetor posição .
(b) Quais são os vetores aceleração nos instantes de velocidade zero? Desenhe estes vetores.
Passo 1
Fala, galera! Vamos resolver essa questão!
O enunciado nos deu um vetor posição e pediu pra gente determinar o vetor aceleração nos instantes em que a velocidade é zero.
Para calcular o vetor velocidade, basta a gente derivar o vetor posição . Em seguida, vamos igualar esse vetor a zero, para descobrir o valor de nos instantes de velocidade zero. Então, derivamos novamente e obtemos o vetor aceleração no ponto .
Vamos lá!
Passo 2
Vamos começar derivando para encontrar o vetor velocidade:
Nos instantes em que a velocidade é nula, cada componente do vetor é nula. Então, vamos igualar cada componente a zero:
Para que o seno de um ângulo seja igual a zero, esse ângulo precisa ser zero ou algum múltiplo de . Então, vamos ter:
Onde .
Passo 3
Derivando , temos o vetor aceleração:
Verificando os vetores aceleração nos instantes de velocidade zero, vamos substituir e nas componentes do vetor :
Poderíamos ter também e assim por diante. Esboçando esse vetor no gráfico, temos:
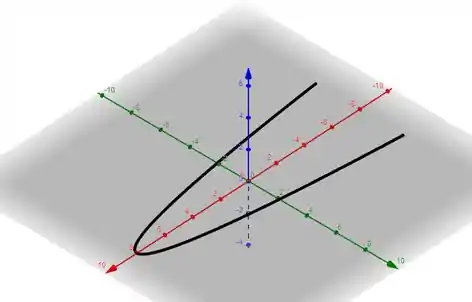
Prontinho, galera! Até a próxima! 😉