Uma partícula se move a partir do ponto em cima da circunferência . Ela dá uma volta no sentido anti-horário, e depois duas no sentido horário. Parametrize a trajetória dessa partícula.
Passo 1
Vamos parametrizar a circunferência, completando quadrados:
Então temos
Passo 2
Agora vamos identificar em que tempo a partícula inicia sua trajetória. Temos
Então
Passo 3
Agora vejamos em que intervalo varia o parâmetro .
A trajetória tem duas partes: na primeira a partícula dá uma volta (rotação de ), e na segunda ela dá duas voltas (rotação de ). E começamos em . Logo:
- 1ª parte da trajetória:
- 2ª parte da trajetória:
Passo 4
Agora temos que ver a questão do sentido de rotação. A 1ª parte se faz no sentido anti-horário, então mantemos o sinal positivo.
Agora, vamos analisar a segunda parte. No instante , quando a partícula começa a se mover no sentido horário, ela se encontra no ponto . Veja a figura abaixo.
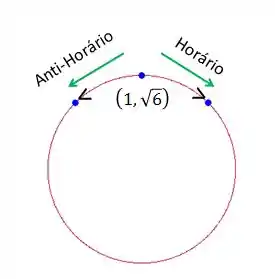
Perceba que, nesse caso, tanto o deslocamento no sentido horário quanto no sentido anti-horário terão em comum a coordenada . Ou seja, não iremos mudar a coordenada da parametrização.
Porém, elas diferem na coordenada . Se a partícula continuasse no sentido anti-horário, estaria indo na direção negativa do eixo , porém no sentido horário ela estaria indo na direção positiva do eixo . Logo, vamos inverter o sinal do cosseno na parametrização.
Então a parametrização da trajetória da partícula é:
Lembrando de não mexer no sinal do ali!! Só trocamos o sinal do cosseno e do seno!