UFRJ, Sem Campus, Cálculo 2, Listas de Cálculo 2 - UFRJ - Lista de Curvas Parametrizadas, Questão 4f
Dê uma parametrização para a curva
A parábola com vértice , foco e diretriz .
(Dica: Uma par��bola com foco e reta diretriz , é constituída de todos os pontos
cuja distância a e a são iguais. A distância de um ponto à é
a distância de ao ponto em mais perto de . Deduza do Teorema de
Pitágoras, que ponto é este.)
Passo 1
Fala galera, tudo bem com vocês? Vamos para mais uma questão de Cálculo 2. Dessa vez estaremos trabalhando curvas parametrizadas.
Nosso objetivo é encontrar uma parametrização para a parábola com vértice , foco e diretriz .
Passo 2
Nosso objetivo é encontrar uma parametrização para a parábola com vértice , foco e diretriz .
Bem, pela definição de foco e diretriz temos que a nossa parábola pode ser dada pelo seguinte desenho:
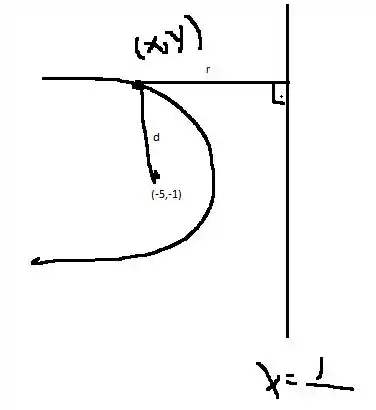
Vamos calcular a coordenada de um ponto qualquer. Pela definição, temos que esse ponto é equidistante ao foco e a reta diretriz. Logo, se é a distância até o foco e a distância até a diretriz, temos que:
Enquanto temos que
Passo 3
Como essas distâncias são iguais
Logo, uma parametrização é
Prontinho pessoal!! Finalizamos mais uma questão. Espero que os passos tenham ficado claros. Até a próxima questão e bons estudos!!!! 😊
Resposta
Desenvolvimento Acima