![]()
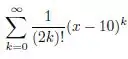
Passo 1
Aqui vamos aplicar o Teste da razão, na forma especial para Séries de potências, ok? Temos o seguinte:
Onde . Vamos aplicar isso no problema:
Então, temos o seguinte limite:
Passo 2
Como , temos:
Ou seja, a série converge para todo
Resposta
![]()
![]()
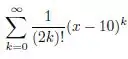
Aqui vamos aplicar o Teste da razão, na forma especial para Séries de potências, ok? Temos o seguinte:
Onde . Vamos aplicar isso no problema:
Então, temos o seguinte limite:
Como , temos:
Ou seja, a série converge para todo
![]()