Calcule a integral de linha onde é o bordo da região delimitada por e , orientado no sentido anti-horário.
Passo 1
Opa! Esse problema nos pede para calcular uma integral de linha
Ao longo de uma curva delimitada por , e orientada no sentido anti-horário. Beleza! Vamos desenhar essa curva doida aí. Como vamos ter temos uma parábola deitada como nessa figura aqui:
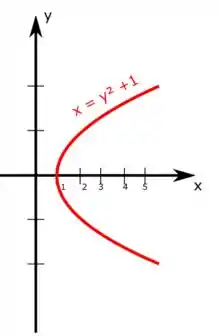
é uma reta vertical no valor 5 de . Juntando essas curvas e orientando a curva no sentido anti-horário temos essa representação aqui:
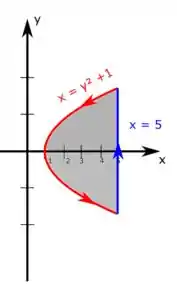
Passo 2
Olha, a integral que o exercício nos dá a gente pode escrever dessa forma aqui
Com
Como a gente representou a curva e viu que ela é uma curva fechada orientada no sentido anti-horário vai ser uma boa usar o teorema de Green:
Onde é a área do interior da curva . Essas derivadas parciais a gente já consegue calcular
Então o teorema de Green nos dá
Passo 3
Agora a gente tem que trazer essa integral
Para algo que a gente consiga resolver. É uma integral dupla e a região de integração é compreendida por
Isso nos diz que a região é uma região do tipo 2 e por isso temos . Nossa integral fica assim
Passo 4
Nossa integral virou uma integral iterada, então a gente pode começar resolvendo a integral de dentro (integral em x) primeiro:
Então a gente obteve
Passo 5
Usando esse resultado na nossa integral temos
Finalmente, resolvendo as integrais em