Use o teorema de Green para determinar o trabalho realizado pelo campo de força
Em uma partícula que inicialmente está no ponto , se move ao longo do eixo para e então se move ao longo da semicircunferência até o ponto inicial.
Passo 1
A primeira coisa que devemos fazer em um exercício como esse, é entender um pouco melhor sobre a curva que estamos querendo trabalhar.
Pra isso, vamos simular a trajetória dessa partícula. Ele disse que ela está inicialmente no ponto :
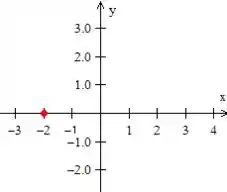
Depois andamos em cima do eixo até o ponto
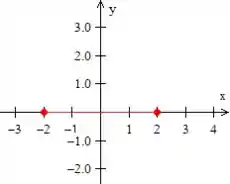
E agora vamos voltar ao ponto de origem pela semicircunferência de raio
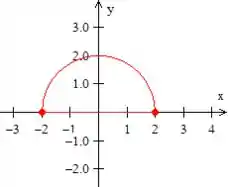
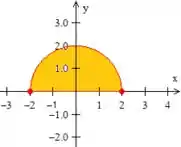
Passo 2
Observe agora que fizemos um caminho fechado e percorremos em um sentido anti-horário (orientação positiva), ou seja, ideal para aplicar o teorema de Green!
Temos por Green que
Essa região da integral dupla, é a região dentro do caminho fechado que percorremos, ou seja o semicírculo
Quanto a essas derivadas parciais, bem....
Passo 3
Essas derivadas parciais aí são o que a gente chama do rotacional do campo, onde a e a são as componentes dele:
então
Calculando essas derivadas parciais
Logo
Passo 4
Retornando para Green...
Agora é só resolver essa integral dupla aí e correr para o abraço! :D
Passo 5
Hummmm! Essa integral dupla aí tem soma de quadrados, além disso, estamos calculando uma integral dupla dentro de um semicírculo, ora, usemos coordenadas polares então:
Uma equação que nos ajuda muito é
não podemos deixar o jacobiano de lado (toda mudança tem ele, lembra?). Em polares ele é
Não podemos prosseguir sem antes os limites desses novos parâmetros.
Passo 6
Como estamos dentro de um semicírculo, dá a metade de uma volta
Quanto ao , bem, ele começa no e termina no raio máximo, que a gente observa ser
Passo 7
Voltando para a integral dupla que devemos resolver
E substituir tudo que obtivemos até agora
Integrando em
Substituindo os limites de integração...
Integrando em agora