Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Exercícios Resolvidos de Teorema de Green

Ver Teoria
Exercício 301234567891011121314151617181920212223242526272829313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100

Enunciado

Questão 4:

A curva de equação x 4 = x 2 - y 2 é chamada de Lemniscata de Gerono. Seu gráfico está esboçado abaixo.

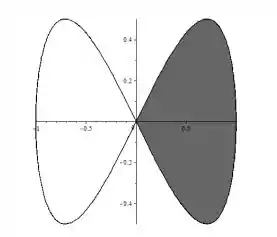
Uma parametrização para a parte da Lemniscata de Gerono que circunda a região colorida na figura acima é

r → t = sin ⁡ t , sin ⁡ t cos ⁡ t ,   0 ≤ t ≤ π

  1. A parametrização acima percorre a curva no sentido horário ou anti-horário? Justifique.
  2. Seja D uma região plana cuja fronteira é uma curva fechada e simples C . Mostre que a área de D pode ser calculada pela fórmula

    3. A D = ∫ C   x d y .

  3. Calcule a área da parte colorida na figura acima.

Passo 1

a )

Que questão interessante! Temos que analisar o sentido de Giro da curva que delimita a região escura. Bem, isso é possível, pois pensa comigo:

t é um parâmetro que varia saindo de 0 e indo até π . Quando o t é 0 ...

r → 0 = sin ⁡ 0 , sin ⁡ 0 cos ⁡ 0 →

r → 0 = 0,0

Quando ele está ainda entre 0 e 90 ° , ou seja...

0 < t < π 2

Tanto o seno quanto o cosseno são positivos...

sin ⁡ t > 0         e         cos ⁡ t > 0

Então o vetor

r → t = sin ⁡ t , sin ⁡ t cos ⁡ t

Será um vetor de coordenadas positivas (no primeiro quadrante). Ora, se você observar a Lemniscata novamente

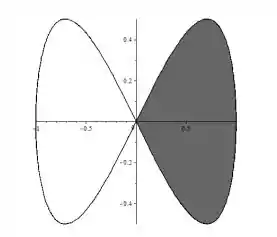
Vai perceber que a única forma de começarmos a curva no 0 ,   0 e a medida que aumentamos o t , primeiro formamos o primeiro quadrante é se a curva estiver girando no sentido horário.

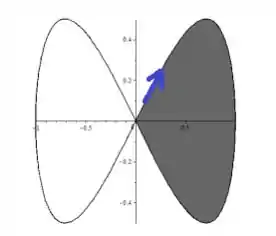
Passo 2

b )

Que fórmula estranha, não é mesmo? Mas vou te dar uma dica, devemos justamente começar a provar isso por ela.

A D = ∫ C   x d y

Repare que embora pareça, a integral não é uma integral simples, afinal estamos calculando a integral na curva C , nos indicando que estamos falando de uma integral de linha:

∫ C   x d y = ∫ C   0   d x + x   d y

HAHA! Melhorou a visualização, neh? É uma integral de linha, onde o campo vetorial é F → x ,   y = 0 ,   x . Outra forma de representa-la como já sabemos é:

∫ C   F → ⋅ d r →

Pois bem, o que agora basicamente vamos fazer é resolver essa integral de linha!

Passo 3

Em uma integral de linha, sabemos que existem deis métodos muito importantes de resolução:

1º - Método Direto.

2º - Teorema de Green.

Infelizmente ou felizmente, não resolveremos pelo método Direto, afinal de contas não temos informação nenhuma sobre a curva C , tirando que ela é uma curva simples, fechada e delimitando uma região D .

Eita!!! A curva é fechada e delimita uma região em seu interior, o que significa que sim, vamos utilizar o Teorema de Green :D , ou seja, sua igualdade linda:

∫ C   F → ⋅ d r → = ∬ D   ∂ Q ∂ x - ∂ P ∂ y d A

Passo 4

O teorema de Green faz algumas exigências antes de aplicarmos sua igualdade:

1º - A curva de ser fechada e delimitando uma região D em seu interior.

Isso já acontece no enunciado.

2º - A curva deve estar orientada positivamente.

Isso significa que ela deve estar girando no sentido anti-horário. Não sabemos se isso é verdade ou não, mas por hora, vamos adotar que sim.

3º - O campo não pode ter singularidades.

F → x ,   y = 0 ,   x

O que também acontece, pois no caso, não temos divisão por zero algum bug do tipo em nenhum lugar do R 2 .

Passo 5

Com essas condições sendo satisfeita, podemos aplicar a igualdade de Green a vontade:

∫ C   F → ⋅ d r → = ∬ D   ∂ Q ∂ x - ∂ P ∂ y d A

Calculando essa subtração de derivadas parciais sabendo que no nosso caso...

F → x ,   y = 0 ⏟ P ,   x ⏟ Q

∂ Q ∂ x - ∂ P ∂ y = 1 - 0 =

1

Logo...

∫ C   F → ⋅ d r → = ∬ D   1 ⋅ d A

HAHA! Quem é a integral dupla de 1   d A ? SIM! A área da região D :

∫ C   F → ⋅ d r → = Á r e a   ( D )

Passo 6

Agora, lembra que colocamos uma condição pra isso ser verdade? A condição é de que a curva C deve estar girando no sentido anti-horário. Mas e se ela não tiver? Bem aí...

∫ C   F → ⋅ d r → = - Á r e a   ( D )

Por isso, para evitar esse problema, colocamos o módulo...

∫ C   x d y = ∫ C   F → ⋅ d r → = A ( D )

Passo 7

c )

Como vimos, podemos calcular a área de duas formas, agora:

1º - Ou calculando pela integral dupla:

∬ D   d A

2º - Ou calculando pela integral de linha do campo F → = 0 ,   x .

∫ C   F → ⋅ d r →

Como a integral dupla seria extremamente chata, pois descrever a Lemniscata não é uma tarefa fácil, vamos aproveitar que a curva já está parametrizada e calcular pela integral de linha!

Passo 8

Para uma integral de linha, como vamos resolver de forma direta, temos três tarefas a cumprir:

1º - Parametrizar a curva C . O que para a nossa alegria, já está...

r → t = sin ⁡ t , sin ⁡ t cos ⁡ t ,   0 ≤ t ≤ π

2º - Substituir os termos da parametrização, já que x = sin ⁡ t e y o outro, na função F → ...

F → x , y = 0 ,   x

F → r → t = 0 , sin ⁡ t

3º - Calcular o termo d r → ...

d r → = r → ' t d t

d r → = sin ⁡ t , sin ⁡ t cos ⁡ t ' d t

d r → = cos ⁡ t , cos ⁡ t cos ⁡ t - sin ⁡ t sin ⁡ t d t

d r → = cos ⁡ t , cos 2 ⁡ t - sin 2 ⁡ t d t

Passo 9

Jogando esses dados na integral de linha que iremos resolver...

∫ C   F → ⋅ d r → = ∫ 0 π 0 , sin ⁡ t ⋅ cos ⁡ t , cos 2 ⁡ t - sin 2 ⁡ t d t =

∫ 0 π sin ⁡ t cos 2 ⁡ t - sin ⁡ t sin 2 ⁡ t d t =

∫ 0 π sin ⁡ t cos 2 ⁡ t - sin ⁡ t 1 - cos 2 ⁡ t d t =

∫ 0 π sin ⁡ t cos 2 ⁡ t - sin ⁡ t + sin ⁡ t cos 2 ⁡ t   d t =

∫ 0 π - sin ⁡ t + 2 sin ⁡ t cos 2 ⁡ t   d t =

Separando as integrais...

∫ 0 π - sin ⁡ t   d t + 2 ∫ 0 π sin ⁡ t cos 2 ⁡ t   d t =

cos ⁡ π - cos ⁡ 0 + 2 ∫ 0 π sin ⁡ t cos 2 ⁡ t   d t =

- 2 + 2 ∫ 0 π sin ⁡ t cos 2 ⁡ t   d t =

Calculando a integral fazendo uma substituição...

cos ⁡ t = a         →             d a = - sin ⁡ t d t     →

sin ⁡ t d t = - d a

Substituindo também a os limites...

t = 0           →               a = cos ⁡ 0 = 1

t = π           →                 a = cos ⁡ π = - 1

- 2 + 2 ∫ 0 π sin ⁡ t cos 2 ⁡ t   d t = - 2 - 2 ∫ 1 - 1 a 2   d a =

Esse menos desaparece se invertermos o os limites...

- 2 + 2 ∫ - 1 1 a 2   d a =

- 2 + 2 a 3 3 - 1 1 = - 2 + 2 1 3 - - 1 3 3 =

- 2 + 4 3 = - 2 3

Então a área é...

A D = ∫ C   F → ⋅ d r → = - 2 3 =

2 3

Resposta

a )

Horário

b )

A D = ∫ C   x d y prova pelo Teorema de Green

c )

A = 2 3

Exercícios de Livros Relacionados

Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas (Fórmula 15.9.9) para o caso onde f x , y = 1 : ∬ R d xd y = ∬ S ∂ x , y ∂ u , v d ud v Aqui, R é
Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = y 2 cos ⁡ x , x 2 + 2 y sen ⁡ x C é o triangulo de 0,0 �� ��a ( 2,6 ) a 2,0 a
Se C é o segmento de reta ligando o ponto ( x 1 , y 1 ) ao ponto ( x 2 , y 2 ) , mostre que ∫ C xd y - yd x = x 1 y 2 - x 2 y 1 Se os vértices de um polígono, na ordem anti-horária, são x 1 , y 1 ,x 2
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y + e x d x + 2 x + cos ⁡ y 2 d y C é a fronteira da região englobada pelas parábolas y = x