Calcule o trabalho do campo vetorial ao longo da curva definida em coordenadas polares por onde , e orientada com crescente.
Passo 1
Essa integral de linha parece complicada de se calcular diretamente pela definição, não é? Não se assuste, ela ficará bem mais simples quando aplicarmos o Teorema de Green.
Bem, pelo enunciado já sabemos que a curva está orientada positivamente, resta, então, saber se ela é fechada. Veja que quando temos , também. Quando aumentamos o valor de , começa aumentar e depois a diminuir, até que em temos novamente . Portanto, em uma variação angular de a curva volta ao mesmo ponto, ou seja, temos uma curva fechada acima do eixo .
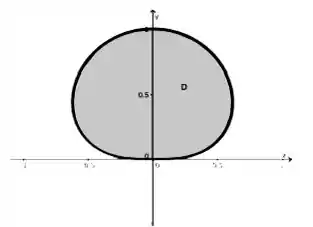
Faremos, então:
Passo 2
Vamos agora calcular :
Passo 3
Aplicando o teorema de Green, temos:
Escrevendo em coordenadas polares essa curva, temos , ou seja, varia entre a origem e a equação da curva. Resta o intervalo de . Como já vimos, a curva volta ao valor com uma variação angular de , temos, então .
Lembre-se de que para aplicarmos o Teorema de Green a curva deve ser percorrida apenas uma vez!
Passo 4
Integrando em relação a :
Passo 5
Aplicando a equação do arco duplo