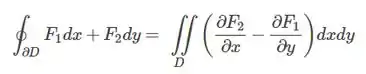Seja um campo de força sobre uma partícula. A partícula inicialmente no ponto (-2,0) se move ao longo do eixo x até (2,0) e então ao longo da semicircunferência até o ponto inicial.
- Utilize o Teorema de Green para determinar o trabalho realizado nessa partícula pelo campo de força
- A integral
é independendo do caminho? Justfique.
Passo 1
- Bom, vamos começar observando para podermos aplicar Green temos que conferir se nossa região está orientada posotivamente e fechada.
- Bom, pra fechar ele nos pergunta se a integral independe do caminho. A resposta pra essa pergunta seria NÃO. Se fosse independente, uma vez que ele sai e volta pra um mesmo ponto, seu trabalho seria NULO, e isso não é oque acontece, como já vimos na letra (a).
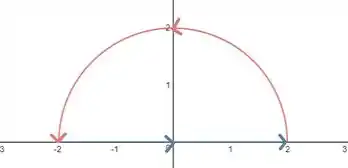
Tudo ok com nossa região então.
Passo 2
Aplicando Green temos que
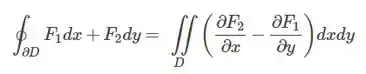
A região D pode ser descita com x variando entre -2 e 2, e y variando entra 0 e
Como estamos trabalhando com uma semi circunferência, facilita nossa vida as coordenadas polares. Então bora lá.
Onde
Passo 3
Agora precisamos encontrar as derivadas do campo!
Colocando isso em coordenadas polares também, ficamos com:
Passo 4
Montando a integral agora, ficamos com (sem esquecer o Jacobiano):
Passo 5
Resposta
Exercícios de Livros Relacionados
Calcule a integral de linha por dois métodos: (a) diretamente e (b) utilizando o Teorema de Green. ∮ C . x 2 y 2 d x + x y d y C consiste num arco de parábola y = x 2 indo de ( 0,0 ) para ( 1,1 ) e o
Utilize o Teorema de Green para demonstrar a fórmula de mudança de variáveis para as integrais duplas (Fórmula 15.9.9) para o caso onde f x , y = 1 : ∬ R d xd y = ∬ S ∂ x , y ∂ u , v d ud v Aqui, R é
Use o teorema de Green para calcular ∫ C F ⋅ d r . (Verifique a orientação da curva antes de aplicar o teorema.) F x , y = y 2 cos x , x 2 + 2 y sen x C é o triangulo de 0,0 �� ��a ( 2,6 ) a 2,0 a
Se C é o segmento de reta ligando o ponto ( x 1 , y 1 ) ao ponto ( x 2 , y 2 ) , mostre que ∫ C xd y - yd x = x 1 y 2 - x 2 y 1 Se os vértices de um polígono, na ordem anti-horária, são x 1 , y 1 ,x 2
Use o Teorema de Green para calcular a integral de linha ao longo da curva dada com orientação positiva. ∫ C y + e x d x + 2 x + cos y 2 d y C é a fronteira da região englobada pelas parábolas y = x